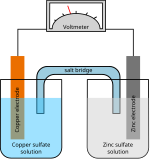
鋅銅電池

丹尼尔电池, 1836年.

裝有鹽橋的丹尼爾電池。

裝有多孔板的丹尼爾電池。
丹尼爾電池又稱锌铜电池,是一种以锌为负電极;铜为正電极;硫酸鋅與硫酸銅為電解液的電化電池[1],由约翰·弗雷德里克·丹尼尔(John Frederic Daniell)於1836年發明,丹尼尔电池一稱來自其发明者的名字,丹尼爾為了消除伏打電堆中出現氫氣泡的問題,他的解決方法是使用第二種電解液來消耗只有一種電解液時會產生的氫氣。
其化学反应式如下[2]:
- Zn(s)+Cu(aq)2+→Zn(aq)2++Cu(s){displaystyle {rm {Zn_{(s)}+Cu_{(aq)}^{2+}rightarrow Zn_{(aq)}^{2+}+Cu_{(s)}}}}
熱力學理論
在熱力學裏,電動勢 E{displaystyle {mathcal {E}}}

dU=TdS−PdV+EdZ{displaystyle mathrm {d} U=Tmathrm {d} S-Pmathrm {d} V+{mathcal {E}}mathrm {d} Z};
其中,U{displaystyle U}




假設電池為丹尼耳電池,由於在這種電池內進行的反應不會產生氣體,系統體積不變,方程式簡化為
dU=TdS+EdZ{displaystyle mathrm {d} U=Tmathrm {d} S+{mathcal {E}}mathrm {d} Z}。
讓熵 S{displaystyle S}


dS=(∂S∂T)ZdT+(∂S∂Z)TdZ{displaystyle mathrm {d} S=left({frac {partial S}{partial T}}right)_{Z}mathrm {d} T+left({frac {partial S}{partial Z}}right)_{T}mathrm {d} Z}。
假設等溫過程,那麼,方程式右手邊的第一個項目等於零:
dS=(∂S∂Z)TdZ{displaystyle mathrm {d} S=left({frac {partial S}{partial Z}}right)_{T}mathrm {d} Z}。
將這方程式帶入內能的方程式:
dU={E+T(∂S∂Z)T}dZ{displaystyle mathrm {d} U=left{{mathcal {E}}+Tleft({frac {partial S}{partial Z}}right)_{T}right}mathrm {d} Z}。
這方程式右手邊的第二個項目是「充電熱」(heat of charging),定義為在一個等溫可逆的充電過程,系統的熱能吸收率 CT(Z){displaystyle C_{T}^{(Z)}}
CT(Z) =def dQTdZ=T(∂S∂Z)T{displaystyle C_{T}^{(Z)} {stackrel {def}{=}} {frac {mathrm {d} Q_{T}}{mathrm {d} Z}}=Tleft({frac {partial S}{partial Z}}right)_{T}}。
吸收率 CT(Z){displaystyle C_{T}^{(Z)}}

dF=dU−d(TS)=−SdT+EdZ{displaystyle mathrm {d} F=mathrm {d} U-mathrm {d} (TS)=-Smathrm {d} T+{mathcal {E}}mathrm {d} Z}。
所以,(E, Z){displaystyle ({mathcal {E}}, Z)}
(∂E∂T)Z=−(∂S∂Z)T{displaystyle left({frac {partial {mathcal {E}}}{partial T}}right)_{Z}=-left({frac {partial S}{partial Z}}right)_{T}}。
帶入內能的方程式:
dU={E−T(∂E∂T)Z}dZ{displaystyle mathrm {d} U=left{{mathcal {E}}-Tleft({frac {partial {mathcal {E}}}{partial T}}right)_{Z}right}mathrm {d} Z}。
通常,電動勢跟溫度 T{displaystyle T}

dU=(E−TdEdT)dZ{displaystyle mathrm {d} U=left({mathcal {E}}-T{frac {mathrm {d} {mathcal {E}}}{mathrm {d} T}}right)mathrm {d} Z}。
對於丹尼耳電池,體積不變,假設等壓過程,則焓的改變 ΔH{displaystyle Delta H}
ΔH=Δ(U+PV)=ΔU{displaystyle Delta H=Delta (U+PV)=Delta U}。
使得一莫耳的金屬原子進入溶液所需要的電荷量為
ΔZ=zNAe{displaystyle Delta Z=zN_{A}e};
其中,z{displaystyle z}


假設恆壓、恆體積,則電池的熱力學性質與電動勢的緊密關係,以方程式表達為
ΔH=zNAe(E−TdEdT){displaystyle Delta H=zN_{A}eleft({mathcal {E}}-T{frac {d{mathcal {E}}}{mathrm {d} T}}right)}。
這樣,只要得到電動勢與溫度之間關係的資料,從測量電動勢和溫度的數據,很容易就能夠準確地計算出某化學反應的反應熱[3]。
参看
- 原电池
参考文献
^ Daniell Cell
^ 可逆电池及其电动势的测定[永久失效連結]
^ Colin B P Finn. Thermal Physics. CRC Press. 1992: 163. ISBN 0748743790.
| |||||||||||||||||||||||||