Brstjjy

Calculation results v t e

Addition (+) summand+summandaddend (broad sense)+addend (broad sense)augend+addend (strict sense)}={displaystyle scriptstyle left.{begin{matrix}scriptstyle {text{summand}},+,{text{summand}}\scriptstyle {text{addend (broad sense)}},+,{text{addend (broad sense)}}\scriptstyle {text{augend}},+,{text{addend (strict sense)}}end{matrix}}right},=,} sum{displaystyle scriptstyle {text{sum}}} Subtraction (−) minuend−subtrahend={displaystyle scriptstyle {text{minuend}},-,{text{subtrahend}},=,} difference{displaystyle scriptstyle {text{difference}}} Multiplication (×) factor×factormultiplier×multiplicand}={displaystyle scriptstyle left.{begin{matrix}scriptstyle {text{factor}},times ,{text{factor}}\scriptstyle {text{multiplier}},times ,{text{multiplicand}}end{matrix}}right},=,} product{displaystyle scriptstyle {text{product}}} Division (÷) dividenddivisor numeratordenominator}={displaystyle scriptstyle left.{begin{matrix}scriptstyle {frac {scriptstyle {text{dividend}}}{scriptstyle {text{divisor}}}}\scriptstyle {text{ }}\scriptstyle {frac {scriptstyle {text{numerator}}}{scriptstyle {text{denominator}}}}end{matrix}}right},=,} fractionquotientratio{displaystyle {begin{matrix}scriptstyle {text{fraction}}\scriptstyle {text{quotient}}\scriptstyle {text{ratio}}end{matrix}}} Exponentiation baseexponent={displaystyle scriptstyle {text{base}}^{text{exponent}},=,} power{displaystyle scriptstyle {text{power}}} nth root (√) radicanddegree={displaystyle scriptstyle {sqrt[{text{degree}}]{scriptstyle {text{radicand}}}},=,} root{displaystyle scriptstyle {text{root}}} Logarithm (log) logbase⁡(antilogarithm)={displaystyle scriptstyle log _{text{base}}({text{antilogarithm}}),=,} logarithm{displaystyle scriptstyle {text{logarithm}}}

In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. Thus, for instance, 6 is the product of 2 and 3 (the result of multiplication), and x⋅(2+x){displaystyle xcdot (2+x)} is the product of x{displaystyle x} and (2+x){displaystyle (2+x)} (indicating that the two factors should be multiplied together).

The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication. When matrices or members of various other associative algebras are multiplied, the product usually depends on the order of the factors. Matrix multiplication, for example, and multiplication in other algebras is in general non-commutative.

There are many different kinds of products in mathematics: besides being able to multiply just numbers, polynomials or matrices, one can also define products on many different algebraic structures. An overview of these different kinds of products is given here.

Product of two numbers

Product of two natural numbers

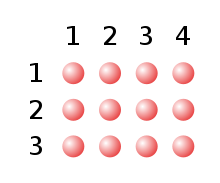
3 by 4 is 12

Placing several stones into a rectangular pattern with r{displaystyle r} rows and s{displaystyle s} columns gives

r⋅s=∑i=1sr=r+r+⋯+r⏟s times=∑j=1rs=s+s+⋯+s⏟r times{displaystyle rcdot s=sum _{i=1}^{s}r=underbrace {r+r+cdots +r} _{s{text{ times}}}=sum _{j=1}^{r}s=underbrace {s+s+cdots +s} _{r{text{ times}}}}

stones. Another approach to multiplication that applies also to real numbers is continuously stretching the number line from 0, so that the 1 is stretched to the one factor, and looking up the product, where the other factor is stretched to.

Product of two integers

Integers allow positive and negative numbers. Their product is determined by the product of their positive amounts, combined with the sign derived from the following rule, which is a necessary consequence of demanding distributivity of the multiplication over addition, but is no additional rule.

⋅−+−+−+−+{displaystyle {begin{array}{|c|c c|}hline cdot &-&+\hline -&+&-\+&-&+\hline end{array}}}

In words, we have:

• Minus times Minus gives Plus


• Minus times Plus gives Minus


• Plus times Minus gives Minus


• Plus times Plus gives Plus

Product of two fractions

Two fractions can be multiplied by multiplying their numerators and denominators:

zn⋅z′n′=z⋅z′n⋅n′{displaystyle {frac {z}{n}}cdot {frac {z'}{n'}}={frac {zcdot z'}{ncdot n'}}}

Product of two real numbers

For a rigorous definition of the product of two real numbers see Construction of the real numbers.

Product of two complex numbers

Two complex numbers can be multiplied by the distributive law and the fact that i2=−1{displaystyle mathrm {i} ^{2}=-1}, as follows:

(a+bi)⋅(c+di)=a⋅c+a⋅di+b⋅ci+b⋅d⋅i2=(a⋅c−b⋅d)+(a⋅d+b⋅c)i{displaystyle {begin{aligned}(a+b,mathrm {i} )cdot (c+d,mathrm {i} )&=acdot c+acdot d,mathrm {i} +bcdot c,mathrm {i} +bcdot dcdot mathrm {i} ^{2}\&=(acdot c-bcdot d)+(acdot d+bcdot c),mathrm {i} end{aligned}}}

Geometric meaning of complex multiplication

A complex number in polar coordinates.

Complex numbers can be written in polar coordinates:

a+bi=r⋅(cos⁡(φ)+isin⁡(φ))=r⋅eiφ{displaystyle a+b,mathrm {i} =rcdot (cos(varphi )+mathrm {i} sin(varphi ))=rcdot mathrm {e} ^{mathrm {i} varphi }}

Furthermore,

c+di=s⋅(cos⁡(ψ)+isin⁡(ψ))=s⋅eiψ{displaystyle c+d,mathrm {i} =scdot (cos(psi )+mathrm {i} sin(psi ))=scdot mathrm {e} ^{mathrm {i} psi }}, from which we obtain:

(a⋅c−b⋅d)+(a⋅d+b⋅c)i=r⋅s⋅(cos⁡(φ+ψ)+isin⁡(φ+ψ))=r⋅s⋅ei(φ+ψ){displaystyle (acdot c-bcdot d)+(acdot d+bcdot c),mathrm {i} =rcdot scdot (cos(varphi +psi )+mathrm {i} sin(varphi +psi ))=rcdot scdot mathrm {e} ^{mathrm {i} (varphi +psi )}}

The geometric meaning is that we multiply the magnitudes and add the angles.

Product of two quaternions

The product of two quaternions can be found in the article on quaternions. However, in this case, a⋅b{displaystyle acdot b} and b⋅a{displaystyle bcdot a} are in general different.

Product of sequences

The product operator for the product of a sequence is denoted by the capital Greek letter pi ∏ (in analogy to the use of the capital Sigma ∑ as summation symbol). The product of a sequence consisting of only one number is just that number itself. The product of no factors at all is known as the empty product, and is equal to 1.

Commutative rings

Commutative rings have a product operation.

Residue classes of integers

Residue classes in the rings Z/NZ{displaystyle mathbb {Z} /Nmathbb {Z} } can be added:

(a+NZ)+(b+NZ)=a+b+NZ{displaystyle (a+Nmathbb {Z} )+(b+Nmathbb {Z} )=a+b+Nmathbb {Z} }

and multiplied:

(a+NZ)⋅(b+NZ)=a⋅b+NZ{displaystyle (a+Nmathbb {Z} )cdot (b+Nmathbb {Z} )=acdot b+Nmathbb {Z} }

Convolution

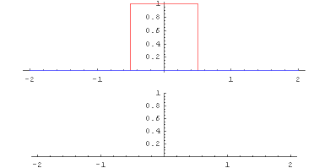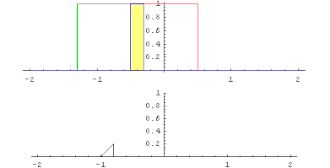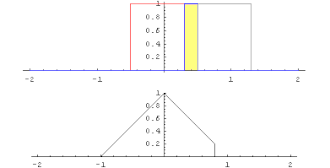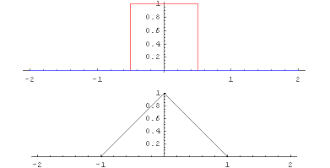
The convolution of the square wave with itself gives the triangular function

Two functions from the reals to itself can be multiplied in another way, called the convolution.

If

∫−∞∞|f(t)|dt<∞and∫−∞∞|g(t)|dt<∞,{displaystyle int limits _{-infty }^{infty }|f(t)|,mathrm {d} t<infty qquad {mbox{and}}qquad int limits _{-infty }^{infty }|g(t)|,mathrm {d} t<infty ,}

then the integral

(f∗g)(t):=∫−∞∞f(τ)⋅g(t−τ)dτ{displaystyle (f*g)(t);:=int limits _{-infty }^{infty }f(tau )cdot g(t-tau ),mathrm {d} tau }

is well defined and is called the convolution.

Under the Fourier transform, convolution becomes point-wise function multiplication.

Polynomial rings

The product of two polynomials is given by the following:

(∑i=0naiXi)⋅(∑j=0mbjXj)=∑k=0n+mckXk{displaystyle left(sum _{i=0}^{n}a_{i}X^{i}right)cdot left(sum _{j=0}^{m}b_{j}X^{j}right)=sum _{k=0}^{n+m}c_{k}X^{k}}

with

ck=∑i+j=kai⋅bj{displaystyle c_{k}=sum _{i+j=k}a_{i}cdot b_{j}}

Products in linear algebra

There are many different kinds of products in linear algebra; some of these have confusingly similar names (outer product, exterior product) but have very different meanings. Others have very different names (outer product, tensor product, Kronecker product) but convey essentially the same idea. A brief overview of these is given here.

Scalar multiplication

By the very definition of a vector space, one can form the product of any scalar with any vector, giving a map R×V→V{displaystyle mathbb {R} times Vrightarrow V}.

Scalar product

A scalar product is a bilinear map:

⋅:V×V→R{displaystyle cdot :Vtimes Vrightarrow mathbb {R} }

with the following conditions, that v⋅v>0{displaystyle vcdot v>0} for all 0≠v∈V{displaystyle 0not =vin V}.

From the scalar product, one can define a norm by letting ‖v‖:=v⋅v{displaystyle |v|:={sqrt {vcdot v}}}.

The scalar product also allows one to define an angle between two vectors:

cos⁡∠(v,w)=v⋅w‖v‖⋅‖w‖{displaystyle cos angle (v,w)={frac {vcdot w}{|v|cdot |w|}}}

In n{displaystyle n}-dimensional Euclidean space, the standard scalar product (called the dot product) is given by:

(∑i=1nαiei)⋅(∑i=1nβiei)=∑i=1nαiβi{displaystyle left(sum _{i=1}^{n}alpha _{i}e_{i}right)cdot left(sum _{i=1}^{n}beta _{i}e_{i}right)=sum _{i=1}^{n}alpha _{i},beta _{i}}

Cross product in 3-dimensional space

The cross product of two vectors in 3-dimensions is a vector perpendicular to the two factors, with length equal to the area of the parallelogram spanned by the two factors.

The cross product can also be expressed as the formal^[a]determinant:

u×v=|ijku1u2u3v1v2v3|{displaystyle mathbf {utimes v} ={begin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \u_{1}&u_{2}&u_{3}\v_{1}&v_{2}&v_{3}\end{vmatrix}}}

Composition of linear mappings

A linear mapping can be defined as a function f between two vector spaces V and W with underlying field F, satisfying^[1]

f(t1x1+t2x2)=t1f(x1)+t2f(x2),∀x1,x2∈V,∀t1,t2∈F.{displaystyle f(t_{1}x_{1}+t_{2}x_{2})=t_{1}f(x_{1})+t_{2}f(x_{2}),forall x_{1},x_{2}in V,forall t_{1},t_{2}in mathbb {F} .}

If one only considers finite dimensional vector spaces, then

f(v)=f(vibVi)=vif(bVi)=fijvibWj,{displaystyle f(mathbf {v} )=f(v_{i}mathbf {b_{V}} ^{i})=v_{i}f(mathbf {b_{V}} ^{i})={f^{i}}_{j}v_{i}mathbf {b_{W}} ^{j},}

in which b_V andb_W denote the bases of V and W, and v_i denotes the component of v on b_Vⁱ, and Einstein summation convention is applied.

Now we consider the composition of two linear mappings between finite dimensional vector spaces. Let the linear mapping f map V to W, and let the linear mapping g map W to U. Then one can get

g∘f(v)=g(fijvibWj)=gjkfijvibUk.{displaystyle gcirc f(mathbf {v} )=g({f^{i}}_{j}v_{i}mathbf {b_{W}} ^{j})={g^{j}}_{k}{f^{i}}_{j}v_{i}mathbf {b_{U}} ^{k}.}

Or in matrix form:

g∘f(v)=GFv,{displaystyle gcirc f(mathbf {v} )=mathbf {G} mathbf {F} mathbf {v} ,}

in which the i-row, j-column element of F, denoted by F_ij, is f^j_i, and G_ij=g^j_i.

The composition of more than two linear mappings can be similarly represented by a chain of matrix multiplication.

Product of two matrices

Given two matrices

A=(ai,j)i=1…s;j=1…r∈Rs×r{displaystyle A=(a_{i,j})_{i=1ldots s;j=1ldots r}in mathbb {R} ^{stimes r}} and B=(bj,k)j=1…r;k=1…t∈Rr×t{displaystyle B=(b_{j,k})_{j=1ldots r;k=1ldots t}in mathbb {R} ^{rtimes t}}

their product is given by

B⋅A=(∑j=1rai,j⋅bj,k)i=1…s;k=1…t∈Rs×t{displaystyle Bcdot A=left(sum _{j=1}^{r}a_{i,j}cdot b_{j,k}right)_{i=1ldots s;k=1ldots t};in mathbb {R} ^{stimes t}}

Composition of linear functions as matrix product

There is a relationship between the composition of linear functions and the product of two matrices. To see this, let r = dim(U), s = dim(V) and t = dim(W) be the (finite) dimensions of vector spaces U, V and W. Let
U={u1,…ur}{displaystyle {mathcal {U}}={u_{1},ldots u_{r}}} be a basis of U,
V={v1,…vs}{displaystyle {mathcal {V}}={v_{1},ldots v_{s}}} be a basis of V and
W={w1,…wt}{displaystyle {mathcal {W}}={w_{1},ldots w_{t}}} be a basis of W. In terms of this basis, let
A=MVU(f)∈Rs×r{displaystyle A=M_{mathcal {V}}^{mathcal {U}}(f)in mathbb {R} ^{stimes r}}
be the matrix representing f : U → V and
B=MWV(g)∈Rr×t{displaystyle B=M_{mathcal {W}}^{mathcal {V}}(g)in mathbb {R} ^{rtimes t}}
be the matrix representing g : V → W. Then

B⋅A=MWU(g∘f)∈Rs×t{displaystyle Bcdot A=M_{mathcal {W}}^{mathcal {U}}(gcirc f)in mathbb {R} ^{stimes t}}

is the matrix representing g∘f:U→W{displaystyle gcirc f:Urightarrow W}.

In other words: the matrix product is the description in coordinates of the composition of linear functions.

Tensor product of vector spaces

Given two finite dimensional vector spaces V and W, the tensor product of them can be defined as a (2,0)-tensor satisfying:

V⊗W(v,m)=V(v)W(w),∀v∈V∗,∀w∈W∗,{displaystyle Votimes W(v,m)=V(v)W(w),forall vin V^{*},forall win W^{*},}

where V^* and W^* denote the dual spaces of V and W.^[2]

For infinite-dimensional vector spaces, one also has the:

• Tensor product of Hilbert spaces


• 
  Topological tensor product.

The tensor product, outer product and Kronecker product all convey the same general idea. The differences between these are that the Kronecker product is just a tensor product of matrices, with respect to a previously-fixed basis, whereas the tensor product is usually given in its intrinsic definition. The outer product is simply the Kronecker product, limited to vectors (instead of matrices).

The class of all objects with a tensor product

In general, whenever one has two mathematical objects that can be combined in a way that behaves like a linear algebra tensor product, then this can be most generally understood as the internal product of a monoidal category. That is, the monoidal category captures precisely the meaning of a tensor product; it captures exactly the notion of why it is that tensor products behave the way they do. More precisely, a monoidal category is the class of all things (of a given type) that have a tensor product.

Other products in linear algebra

Other kinds of products in linear algebra include:

• Hadamard product


• Kronecker product


• The product of tensors:
  
  
  
  • Wedge product or exterior product
  
  
  • Interior product
  
  
  • Outer product
  
  
  • Tensor product
  
  
  
  

Cartesian product

In set theory, a Cartesian product is a mathematical operation which returns a set (or product set) from multiple sets. That is, for sets A and B, the Cartesian product A × B is the set of all ordered pairs (a, b) where a ∈ A and b ∈ B.^[3]

The class of all things (of a given type) that have Cartesian products is called a Cartesian category. Many of these are Cartesian closed categories. Sets are an example of such objects.

Empty product

The empty product on numbers and most algebraic structures has the value of 1 (the identity element of multiplication) just like the empty sum has the value of 0 (the identity element of addition). However, the concept of the empty product is more general, and requires special treatment in logic, set theory, computer programming and category theory.

Products over other algebraic structures

Products over other kinds of algebraic structures include:

• the Cartesian product of sets


• the direct product of groups, and also the semidirect product, knit product and wreath product
  


• the free product of groups


• the product of rings
  


• the product of ideals
  


• the product of topological spaces
  


• the Wick product of random variables
  


• the cap, cup, Massey and slant product in algebraic topology


• the smash product and wedge sum (sometimes called the wedge product) in homotopy
  

A few of the above products are examples of the general notion of an internal product in a monoidal category; the rest are describable by the general notion of a product in category theory.

Products in category theory

All of the previous examples are special cases or examples of the general notion of a product. For the general treatment of the concept of a product, see product (category theory), which describes how to combine two objects of some kind to create an object, possibly of a different kind. But also, in category theory, one has:

• the fiber product or pullback,


• the product category, a category that is the product of categories.


• the ultraproduct, in model theory.


• the internal product of a monoidal category, which captures the essence of a tensor product.

Other products

• A function's product integral (as a continuous equivalent to the product of a sequence or as the multiplicative version of the (normal/standard/additive) integral. The product integral is also known as "continuous product" or "multiplical".


• 
  Complex multiplication, a theory of elliptic curves.

See also

• Deligne tensor product of abelian categories


• Iterated binary operation


• Multiplicative calculus

Notes

References

External links

• 
  Product on Wolfram Mathworld
  


• 
  "Product". PlanetMath.