库利－图基快速傅里叶变换算法





库利－图基快速傅里叶变换算法（Cooley-Tukey算法）[1]是最常見的快速傅里葉變換算法。這一方法以分治法為策略遞歸地將長度為N = N1N2的DFT分解為長度分別為N1和N2的兩個較短序列的DFT，以及與旋轉因子的複數乘法。這種方法以及FFT的基本思路在1965年J. W. Cooley和J. W. Tukey合作發表An algorithm for the machine calculation of complex Fourier series之後開始為人所知。但後來發現，實際上這兩位作者只是重新發明了高斯在1805年就已經提出的算法（此算法在歷史上數次以各種形式被再次提出）。


库利－图基算法最有名的應用，是將序列長為N的DFT分割為兩個長為N/2的子序列的DFT，因此這一應用只適用於序列長度為2的冪的DFT計算，即基2-FFT。實際上，如同高斯和库利與图基都指出的那樣，库利－图基算法也可以用於序列長度N為任意因數分解形式的DFT，即混合基FFT，而且還可以應用於其他諸如分裂基FFT等變種。儘管库利－图基算法的基本思路是採用遞歸的方法進行計算，大多數傳統的算法實現都將顯示的遞歸算法改寫為非遞歸的形式。另外，因為库利－图基算法是將DFT分解為較小長度的多個DFT，因此它可以同任一種其他的DFT算法聯合使用。




目录






  • 1 複雜度


  • 2 時域/頻域抽取法


    • 2.1 時域抽取法


    • 2.2 頻域抽取法




  • 3 單一基底


    • 3.1 2基底


    • 3.2 4基底


    • 3.3 8基底




  • 4 混合基底


    • 4.1 2/8基底


    • 4.2 2/4/8基底


    • 4.3 22基底


    • 4.4 23基底


      • 4.4.1 22{displaystyle {frac {sqrt {2}}{2}}}{frac {sqrt {2}}{2}}乘法化簡






  • 5 參考資料





複雜度


離散傅立葉變換的複雜度為O(n2){displaystyle {mathcal {O}}(n^{2})}{mathcal {O}}(n^{2})（可參考大O符號）


快速傅立葉變換的複雜度為O(Nlog⁡N){displaystyle {mathcal {O}}(Nlog N)}{mathcal {O}}(Nlog N)，分析可見下方架構圖部分，級數為log⁡N{displaystyle log N}log N而每一級的複雜度為N{displaystyle N}N，故複雜度為O(Nlog⁡N){displaystyle {mathcal {O}}(Nlog N)}{mathcal {O}}(Nlog N)



時域/頻域抽取法


在FFT演算法中，針對輸入做不同方式的分組會造成輸出順序上的不同。如果我們使用時域抽取（Decimation-in-time），那麼輸入的順序將會是位元反轉排列（bit-reversed order），輸出將會依序排列。但若我們採取的是頻域抽取（Decimation-in-frequency），那麼輸出與輸出順序的情況將會完全相反，變為依序排列的輸入與位元反轉排列的輸出。


DIT與DIF的在8點FFT下的架構對照圖



時域抽取法


我們可以將DFT公式中的項目在時域上重新分組，這樣就叫做時域抽取（Decimation-in-time），在這裡e−j(2πnkN){displaystyle e^{-j(2pi {frac {nk}{N}})}}e^{-j(2pi {frac {nk}{N}})}將會被代換為旋轉因子（twiddle factor）WNnk{displaystyle W_{N}^{nk}}W_{N}^{nk}。


X[k]=∑n=0N−1x[n]e−j(2πnkN)k=0,1,…,N−1{displaystyle X[k]=sum _{n=0}^{N-1}x[n]e^{-j(2pi {frac {nk}{N}})}qquad k=0,1,ldots ,N-1}X[k]=sum _{n=0}^{N-1}x[n]e^{-j(2pi {frac {nk}{N}})}qquad k=0,1,ldots ,N-1


=∑n evenx[n]WNnk+∑n oddx[n]WNnk{displaystyle =sum _{n even}x[n]W_{N}^{nk}+sum _{n odd}x[n]W_{N}^{nk}}=sum _{n even}x[n]W_{N}^{nk}+sum _{n odd}x[n]W_{N}^{nk}


=∑r=0(N/2)−1x[2r]WN2rk+∑r=0(N/2)−1x[2r+1]WN(2r+1)k{displaystyle =sum _{r=0}^{(N/2)-1}x[2r]W_{N}^{2rk}+sum _{r=0}^{(N/2)-1}x[2r+1]W_{N}^{(2r+1)k}}=sum _{r=0}^{(N/2)-1}x[2r]W_{N}^{2rk}+sum _{r=0}^{(N/2)-1}x[2r+1]W_{N}^{(2r+1)k}


=∑r=0(N/2)−1x[2r]WN2rk+WNk∑r=0(N/2)−1x[2r+1]WN2rk{displaystyle =sum _{r=0}^{(N/2)-1}x[2r]W_{N}^{2rk}+W_{N}^{k}sum _{r=0}^{(N/2)-1}x[2r+1]W_{N}^{2rk}}=sum _{r=0}^{(N/2)-1}x[2r]W_{N}^{2rk}+W_{N}^{k}sum _{r=0}^{(N/2)-1}x[2r+1]W_{N}^{2rk}


=∑r=0(N/2)−1x[2r]WN/2rk+WNk∑r=0(N/2)−1x[2r+1]WN/2rk{displaystyle =sum _{r=0}^{(N/2)-1}x[2r]W_{N/2}^{rk}+W_{N}^{k}sum _{r=0}^{(N/2)-1}x[2r+1]W_{N/2}^{rk}}=sum _{r=0}^{(N/2)-1}x[2r]W_{N/2}^{rk}+W_{N}^{k}sum _{r=0}^{(N/2)-1}x[2r+1]W_{N/2}^{rk}


=G[k]+WNkH[k]{displaystyle =G[k]+W_{N}^{k}H[k]}=G[k]+W_{N}^{k}H[k]


在這邊我們要注意的是，我們所替換的G[k]與H[k]具有週期性：


  • {G[k+N2]=G[k]H[k+N2]=H[k]{displaystyle {begin{cases}G[k+{frac {N}{2}}]=G[k]\H[k+{frac {N}{2}}]=H[k]end{cases}}}{begin{cases}G[k+{frac {N}{2}}]=G[k]\H[k+{frac {N}{2}}]=H[k]end{cases}}

上述的推導可以劃成下面的圖：


DIT N8.JPG


劃紅框處所示的N2{displaystyle {frac {N}{2}}}{frac {N}{2}}點DFT架構如下圖所示：


DIT N4.JPG


劃紅框處所示的N4{displaystyle {frac {N}{4}}}{frac {N}{4}}點DFT架構如下圖所示：


DIT N2.JPG


下圖是一個8點DIT FFT的完整架構圖。


DIT N8 ALL.JPG



頻域抽取法


我們可以將DFT公式中的項目在頻域上重新分組，這樣就叫做頻域抽取（Decimation-in-frequency）。


首先先觀察在頻域上偶數項的部分：


X[2r]=∑n=0N−1x[n]WNn(2r) r=0,1,⋯,N2−1{displaystyle X[2r]=sum _{n=0}^{N-1}x[n]W_{N}^{n(2r)} r=0,1,cdots ,{frac {N}{2}}-1}X[2r]=sum _{n=0}^{N-1}x[n]W_{N}^{n(2r)} r=0,1,cdots ,{frac {N}{2}}-1


=∑n=0N2−1x[n]WN2nr+∑n=N2N−1x[n]WN2nr{displaystyle =sum _{n=0}^{{frac {N}{2}}-1}x[n]W_{N}^{2nr}+sum _{n={frac {N}{2}}}^{N-1}x[n]W_{N}^{2nr}}=sum _{n=0}^{{frac {N}{2}}-1}x[n]W_{N}^{2nr}+sum _{n={frac {N}{2}}}^{N-1}x[n]W_{N}^{2nr}


=∑n=0N2−1x[n]WN2nr+∑n=0N2−1x[n+N2]WN2r[n+N2]{displaystyle =sum _{n=0}^{{frac {N}{2}}-1}x[n]W_{N}^{2nr}+sum _{n=0}^{{frac {N}{2}}-1}x[n+{frac {N}{2}}]W_{N}^{2r[n+{frac {N}{2}}]}}=sum _{n=0}^{{frac {N}{2}}-1}x[n]W_{N}^{2nr}+sum _{n=0}^{{frac {N}{2}}-1}x[n+{frac {N}{2}}]W_{N}^{2r[n+{frac {N}{2}}]}


∵WN2r[n+N2]=WN2rnWNrN=WN2rn{displaystyle {color {Gray}because W_{N}^{2r[n+{frac {N}{2}}]}=W_{N}^{2rn}W_{N}^{rN}=W_{N}^{2rn}}}{color {Gray}because W_{N}^{2r[n+{frac {N}{2}}]}=W_{N}^{2rn}W_{N}^{rN}=W_{N}^{2rn}}


=∑n=0N2−1x[n]WN2rn+∑n=0N2−1x[n+N2]WN2rn{displaystyle =sum _{n=0}^{{frac {N}{2}}-1}x[n]W_{N}^{2rn}+sum _{n=0}^{{frac {N}{2}}-1}x[n+{frac {N}{2}}]W_{N}^{2rn}}=sum _{n=0}^{{frac {N}{2}}-1}x[n]W_{N}^{2rn}+sum _{n=0}^{{frac {N}{2}}-1}x[n+{frac {N}{2}}]W_{N}^{2rn}


=∑n=0N2−1(x[n]+x[n+N2])WN2rn{displaystyle =sum _{n=0}^{{frac {N}{2}}-1}(x[n]+x[n+{frac {N}{2}}])W_{frac {N}{2}}^{rn}}=sum _{n=0}^{{frac {N}{2}}-1}(x[n]+x[n+{frac {N}{2}}])W_{frac {N}{2}}^{rn}


=∑n=0N2−1g[n]WN2rn{displaystyle =sum _{n=0}^{{frac {N}{2}}-1}g[n]W_{frac {N}{2}}^{rn}}=sum _{n=0}^{{frac {N}{2}}-1}g[n]W_{frac {N}{2}}^{rn}


再觀察在頻域上奇數項的部分：


X[2r+1]=∑n=0N−1x[n]WNn(2r+1) r=0,1,⋯,N2−1{displaystyle X[2r+1]=sum _{n=0}^{N-1}x[n]W_{N}^{n(2r+1)} r=0,1,cdots ,{frac {N}{2}}-1}X[2r+1]=sum _{n=0}^{N-1}x[n]W_{N}^{n(2r+1)} r=0,1,cdots ,{frac {N}{2}}-1


=∑n=0N2−1x[n]WNn(2r+1)+∑n=N2N−1x[n]WNn(2r+1){displaystyle =sum _{n=0}^{{frac {N}{2}}-1}x[n]W_{N}^{n(2r+1)}+sum _{n={frac {N}{2}}}^{N-1}x[n]W_{N}^{n(2r+1)}}=sum _{n=0}^{{frac {N}{2}}-1}x[n]W_{N}^{n(2r+1)}+sum _{n={frac {N}{2}}}^{N-1}x[n]W_{N}^{n(2r+1)}


=∑n=0N2−1x[n]WNn(2r+1)+∑n=0N2−1x[n+N2]WN(2r+1)[n+N2]{displaystyle =sum _{n=0}^{{frac {N}{2}}-1}x[n]W_{N}^{n(2r+1)}+sum _{n=0}^{{frac {N}{2}}-1}x[n+{frac {N}{2}}]W_{N}^{(2r+1)[n+{frac {N}{2}}]}}=sum _{n=0}^{{frac {N}{2}}-1}x[n]W_{N}^{n(2r+1)}+sum _{n=0}^{{frac {N}{2}}-1}x[n+{frac {N}{2}}]W_{N}^{(2r+1)[n+{frac {N}{2}}]}


∵WN(2r+1)[n+N2]=WN(2r+1)nWN(2r+1)N2=−WN(2r+1)n{displaystyle {color {Gray}because W_{N}^{(2r+1)[n+{frac {N}{2}}]}=W_{N}^{(2r+1)n}W_{N}^{(2r+1){frac {N}{2}}}=-W_{N}^{(2r+1)n}}}{color {Gray}because W_{N}^{(2r+1)[n+{frac {N}{2}}]}=W_{N}^{(2r+1)n}W_{N}^{(2r+1){frac {N}{2}}}=-W_{N}^{(2r+1)n}}


=∑n=0N2−1x[n]WN(2r+1)n−∑n=0N2−1x[n+N2]WN(2r+1)n{displaystyle =sum _{n=0}^{{frac {N}{2}}-1}x[n]W_{N}^{(2r+1)n}-sum _{n=0}^{{frac {N}{2}}-1}x[n+{frac {N}{2}}]W_{N}^{(2r+1)n}}=sum _{n=0}^{{frac {N}{2}}-1}x[n]W_{N}^{(2r+1)n}-sum _{n=0}^{{frac {N}{2}}-1}x[n+{frac {N}{2}}]W_{N}^{(2r+1)n}


=∑n=0N2−1(x[n]−x[n+N2])WNn(2r+1){displaystyle =sum _{n=0}^{{frac {N}{2}}-1}(x[n]-x[n+{frac {N}{2}}])W_{N}^{n(2r+1)}}=sum _{n=0}^{{frac {N}{2}}-1}(x[n]-x[n+{frac {N}{2}}])W_{N}^{n(2r+1)}


=∑n=0N2−1(x[n]−x[n+N2])WNnWN2nr{displaystyle =sum _{n=0}^{{frac {N}{2}}-1}(x[n]-x[n+{frac {N}{2}}])W_{N}^{n}W_{frac {N}{2}}^{nr}}=sum _{n=0}^{{frac {N}{2}}-1}(x[n]-x[n+{frac {N}{2}}])W_{N}^{n}W_{frac {N}{2}}^{nr}


=∑n=0N2−1(h[n]WNn)WN2rn{displaystyle =sum _{n=0}^{{frac {N}{2}}-1}(h[n]W_{N}^{n})W_{frac {N}{2}}^{rn}}=sum _{n=0}^{{frac {N}{2}}-1}(h[n]W_{N}^{n})W_{frac {N}{2}}^{rn}


上述的推導可以畫成下面的圖：


DIF N8.JPG


更進一步的拆解N2{displaystyle {frac {N}{2}}}{frac {N}{2}}-point DFT的架構


DIF N4.JPG


下圖為8點FFT下N4{displaystyle {frac {N}{4}}}{frac {N}{4}}-point DFT的架構


DIF N2.JPG


總結上述架構，完整的8點DIF FFT架構圖為


DIF N8 ALL.JPG



單一基底


利用库利－图基演算法進行離散傅立葉拆解時，能夠依需求而以2, 4, 8…等2的冪次方為單位進行拆解，不同的拆解方法會產生不同層數快速傅里葉變換的架構，基底越大則層數越少，複數乘法器也越少，但是每級的蝴蝶形架構則會越複雜，因此常見的架構為2基底、4基底與8基底這三種設計。



2基底


2基底-快速傅立葉演算法（Radix-2 FFT）是最廣為人知的一種库利－图基快速傅立葉演算法分支。此方法不斷地將N點的FFT拆解成兩個'N/2'點的FFT，利用旋轉因子Wnk,WN2{displaystyle W^{nk},W^{frac {N}{2}}}W^{nk},W^{frac {N}{2}}的對稱性藉此來降低DFT的計算複雜度，達到加速的功效。


而其實前述有關時域抽取或是頻域抽取的方法介紹，即為2基底的快速傅立葉轉換法。以下展示其他種2基底快速傅立葉演算法的連線方法，此種不規則的連線方法可以讓輸出與輸入都為循序排列，但是連線的複雜度卻大大的增加。


Radix-2 Alt1.jpg


Radix-2 Alt2.jpg



4基底


4基底快速傅立葉變換演算法則是承接2基底的概念，在此裡用時域抽取的技巧，將原本的DFT公式拆解為四個一組的形式：


X[k]=∑n=0N−1x[n]e−j(2πnkN)k=0,1,…,N−1{displaystyle X[k]=sum _{n=0}^{N-1}x[n]e^{-j(2pi {frac {nk}{N}})}qquad k=0,1,ldots ,N-1}X[k]=sum _{n=0}^{N-1}x[n]e^{-j(2pi {frac {nk}{N}})}qquad k=0,1,ldots ,N-1


=∑n=0N4−1x[4n+0]WN(4n+0)k+∑n=0N4−1x[4n+1]WN(4n+1)k{displaystyle =sum _{n=0}^{{frac {N}{4}}-1}x[4n+0]W_{N}^{(4n+0)k}+sum _{n=0}^{{frac {N}{4}}-1}x[4n+1]W_{N}^{(4n+1)k}}=sum _{n=0}^{{frac {N}{4}}-1}x[4n+0]W_{N}^{(4n+0)k}+sum _{n=0}^{{frac {N}{4}}-1}x[4n+1]W_{N}^{(4n+1)k}


+∑n=0N4−1x[4n+2]WN(4n+2)k+∑n=0N4−1x[4n+3]WN(4n+3)k{displaystyle +sum _{n=0}^{{frac {N}{4}}-1}x[4n+2]W_{N}^{(4n+2)k}+sum _{n=0}^{{frac {N}{4}}-1}x[4n+3]W_{N}^{(4n+3)k}}+sum _{n=0}^{{frac {N}{4}}-1}x[4n+2]W_{N}^{(4n+2)k}+sum _{n=0}^{{frac {N}{4}}-1}x[4n+3]W_{N}^{(4n+3)k}


=WN0∑n=0N4−1x[4n+0]WN4nk+WN1k∑n=0N4−1x[4n+1]WN4nk{displaystyle =W_{N}^{0}sum _{n=0}^{{frac {N}{4}}-1}x[4n+0]W_{frac {N}{4}}^{nk}+W_{N}^{1k}sum _{n=0}^{{frac {N}{4}}-1}x[4n+1]W_{frac {N}{4}}^{nk}}{displaystyle =W_{N}^{0}sum _{n=0}^{{frac {N}{4}}-1}x[4n+0]W_{frac {N}{4}}^{nk}+W_{N}^{1k}sum _{n=0}^{{frac {N}{4}}-1}x[4n+1]W_{frac {N}{4}}^{nk}}


+WN2k∑n=0N4−1x[4n+2]WN4nk+WN3k∑n=0N4−1x[4n+3]WN4nk{displaystyle +W_{N}^{2k}sum _{n=0}^{{frac {N}{4}}-1}x[4n+2]W_{frac {N}{4}}^{nk}+W_{N}^{3k}sum _{n=0}^{{frac {N}{4}}-1}x[4n+3]W_{frac {N}{4}}^{nk}}{displaystyle +W_{N}^{2k}sum _{n=0}^{{frac {N}{4}}-1}x[4n+2]W_{frac {N}{4}}^{nk}+W_{N}^{3k}sum _{n=0}^{{frac {N}{4}}-1}x[4n+3]W_{frac {N}{4}}^{nk}}


WN0F0(k)+WNkF1(k)+WN2kF2(k)+WN3kF3(k){displaystyle W_{N}^{0}F_{0}(k)+W_{N}^{k}F_{1}(k)+W_{N}^{2k}F_{2}(k)+W_{N}^{3k}F_{3}(k)}{displaystyle W_{N}^{0}F_{0}(k)+W_{N}^{k}F_{1}(k)+W_{N}^{2k}F_{2}(k)+W_{N}^{3k}F_{3}(k)}


在這裡再利用Wnk+N4=−Wnk+3N4=−jWnk{displaystyle W^{nk+{frac {N}{4}}}=-W^{nk+{frac {3N}{4}}}=-jW^{nk}}W^{nk+{frac {N}{4}}}=-W^{nk+{frac {3N}{4}}}=-jW^{nk}的特性來進行與2基數FFT類似的化減方法，以降低演算法複雜度。



8基底


在库利－图基算法裡，使用的基底（radix）越大，複數的乘法與記憶體的存取就越少，所帶來的好處不言而喻。但是隨之而來的就是實數的乘法與實數的加法也會增加，尤其計算單元的設計也就越複雜，對於可應用FFT之點數限制也就越嚴格。在表中我們可以看到在不同基底下所需的計算成本。










































使用4096點FFT在不同基底下的計算量
動作 2基底 4基底 8基底
複數乘法
 22528 15360 10752
實數乘法
 0 0 8192
複數加法
 49152 49152 49152
實數加法
 0 0 8192
記憶體存取
 49152 24576 16384

在DFT的公式中，我們重新定義x=[x(0),x(1),…,x(N-1)]T, X=[X(0),X(1),…,X(N-1)]T，則DFT可重寫為X=FN‧x。FN是一個N×N的DFT矩陣，其元素定義為[FN]ij=WNij(i,j ∈ [0,N-1])，當N=8時，我們可以得到以下的F8矩陣並且進一步將其拆解。


在拆解成三個矩陣相乘之後，我們可以將複數運算的數量從56個降至24個複數的加法。底下是8基底的的SFG。要注意的是所有的輸出與輸入都是複數的形式，而輸出與輸入的排序也並非規律排列，此種排列方式是為了要達到接線的最佳化。


8基底FFT演算法用於8點FFT的SFG



混合基底



2/8基底


在2/8基底的演算法中，我們可以看到我們對於偶數項的輸出會使用2基底的分解法，對於奇數項的輸出採用8基底的分解法。這個做法充分利用了2基底與4基底擁有最少乘法數與加法數的特性。當使用了2基底的分解法後，偶數項的輸出如下所示。


C2k=∑n=0N2−1(x2n+xN2+n)W2nk{displaystyle C_{2k}=sum _{n=0}^{{frac {N}{2}}-1}(x_{2n}+x_{{frac {N}{2}}+n})W^{2nk}}C_{2k}=sum _{n=0}^{{frac {N}{2}}-1}(x_{2n}+x_{{frac {N}{2}}+n})W^{2nk}


奇數項的輸出則交由8基底分解來處理，如下四式所述。


C8k+1=∑n=0N8−1{[(xn−xn+N2)−j(xn+N4−xn+3N4)]+WN8[(xn+N8−xn+5N8)−j(xn+3N8−xn+7N8)]}W8nkWn{displaystyle C_{8k+1}=sum _{n=0}^{{frac {N}{8}}-1}{begin{Bmatrix}[(x_{n}-x_{n+{frac {N}{2}}})-j(x_{n+{frac {N}{4}}}-x_{n+{frac {3N}{4}}})]+W^{frac {N}{8}}[(x_{n+{frac {N}{8}}}-x_{n+{frac {5N}{8}}})-j(x_{n+{frac {3N}{8}}}-x_{n+{frac {7N}{8}}})]end{Bmatrix}}W^{8nk}W^{n}}C_{8k+1}=sum _{n=0}^{{frac {N}{8}}-1}{begin{Bmatrix}[(x_{n}-x_{n+{frac {N}{2}}})-j(x_{n+{frac {N}{4}}}-x_{n+{frac {3N}{4}}})]+W^{frac {N}{8}}[(x_{n+{frac {N}{8}}}-x_{n+{frac {5N}{8}}})-j(x_{n+{frac {3N}{8}}}-x_{n+{frac {7N}{8}}})]end{Bmatrix}}W^{8nk}W^{n}


C8k+5=∑n=0N8−1{[(xn−xn+N2)−j(xn+N4−xn+3N4)]−WN8[(xn+N8−xn+5N8)−j(xn+3N8−xn+7N8)]}W8nkW5n{displaystyle C_{8k+5}=sum _{n=0}^{{frac {N}{8}}-1}{begin{Bmatrix}[(x_{n}-x_{n+{frac {N}{2}}})-j(x_{n+{frac {N}{4}}}-x_{n+{frac {3N}{4}}})]-W^{frac {N}{8}}[(x_{n+{frac {N}{8}}}-x_{n+{frac {5N}{8}}})-j(x_{n+{frac {3N}{8}}}-x_{n+{frac {7N}{8}}})]end{Bmatrix}}W^{8nk}W^{5n}}C_{8k+5}=sum _{n=0}^{{frac {N}{8}}-1}{begin{Bmatrix}[(x_{n}-x_{n+{frac {N}{2}}})-j(x_{n+{frac {N}{4}}}-x_{n+{frac {3N}{4}}})]-W^{frac {N}{8}}[(x_{n+{frac {N}{8}}}-x_{n+{frac {5N}{8}}})-j(x_{n+{frac {3N}{8}}}-x_{n+{frac {7N}{8}}})]end{Bmatrix}}W^{8nk}W^{5n}


C8k+3=∑n=0N8−1{[(xn−xn+N2)+j(xn+N4−xn+3N4)]+W3N8[(xn+N8−xn+5N8)+j(xn+3N8−xn+7N8)]}W8nkW3n{displaystyle C_{8k+3}=sum _{n=0}^{{frac {N}{8}}-1}{begin{Bmatrix}[(x_{n}-x_{n+{frac {N}{2}}})+j(x_{n+{frac {N}{4}}}-x_{n+{frac {3N}{4}}})]+W^{frac {3N}{8}}[(x_{n+{frac {N}{8}}}-x_{n+{frac {5N}{8}}})+j(x_{n+{frac {3N}{8}}}-x_{n+{frac {7N}{8}}})]end{Bmatrix}}W^{8nk}W^{3n}}C_{8k+3}=sum _{n=0}^{{frac {N}{8}}-1}{begin{Bmatrix}[(x_{n}-x_{n+{frac {N}{2}}})+j(x_{n+{frac {N}{4}}}-x_{n+{frac {3N}{4}}})]+W^{frac {3N}{8}}[(x_{n+{frac {N}{8}}}-x_{n+{frac {5N}{8}}})+j(x_{n+{frac {3N}{8}}}-x_{n+{frac {7N}{8}}})]end{Bmatrix}}W^{8nk}W^{3n}


C8k+7=∑n=0N8−1{[(xn−xn+N2)+j(xn+N4−xn+3N4)]−W3N8[(xn+N8−xn+5N8)+j(xn+3N8−xn+7N8)]}W8nkW7n{displaystyle C_{8k+7}=sum _{n=0}^{{frac {N}{8}}-1}{begin{Bmatrix}[(x_{n}-x_{n+{frac {N}{2}}})+j(x_{n+{frac {N}{4}}}-x_{n+{frac {3N}{4}}})]-W^{frac {3N}{8}}[(x_{n+{frac {N}{8}}}-x_{n+{frac {5N}{8}}})+j(x_{n+{frac {3N}{8}}}-x_{n+{frac {7N}{8}}})]end{Bmatrix}}W^{8nk}W^{7n}}C_{8k+7}=sum _{n=0}^{{frac {N}{8}}-1}{begin{Bmatrix}[(x_{n}-x_{n+{frac {N}{2}}})+j(x_{n+{frac {N}{4}}}-x_{n+{frac {3N}{4}}})]-W^{frac {3N}{8}}[(x_{n+{frac {N}{8}}}-x_{n+{frac {5N}{8}}})+j(x_{n+{frac {3N}{8}}}-x_{n+{frac {7N}{8}}})]end{Bmatrix}}W^{8nk}W^{7n}


以上式子就是2/8基底的FFT快速演算法。在架構圖上可化為L型的蝴蝶運算架構，如下圖所示。


Radix-2 8-Butterfly.png


而下圖表示的是一個64點的FFT使用2/8基底的架構圖。雖然2/8基底的演算法縮減了WN8,W3N8{displaystyle W^{frac {N}{8}},W^{frac {3N}{8}}}W^{frac {N}{8}},W^{frac {3N}{8}}的乘法量，但是這種演算法最大的缺點是跟其他固定基底或是混合基底比較起來，他的架構較為不規則。所以在硬體上比4基底或是2基底更難實現。


Radix-2 8-64-point.png



2/4/8基底


為了改進Radix 2/8在架構上的不規則性，我們在這裡做了一些修改，如下圖4.。此修改可讓架構更加規則，且所使用的加法器與乘法器數量更加減少，如下表所示。









































8n點FFT在不同演算法下所需複數乘法量
N=8n
 2基底 4基底 2/4混合基底 2/4/8基底
8
 2 - 2 0
64
 98 76 72 48
512
 1538 - 1082 824
4096
 18434 13996 12774 10168

在這裡我們最小的運算單元稱為PE（Process Element）,PE內部包含了2/8基底、2/4基底、2基底的運算，簡化過的信號處理流程與蝴蝶型架構圖可見下圖


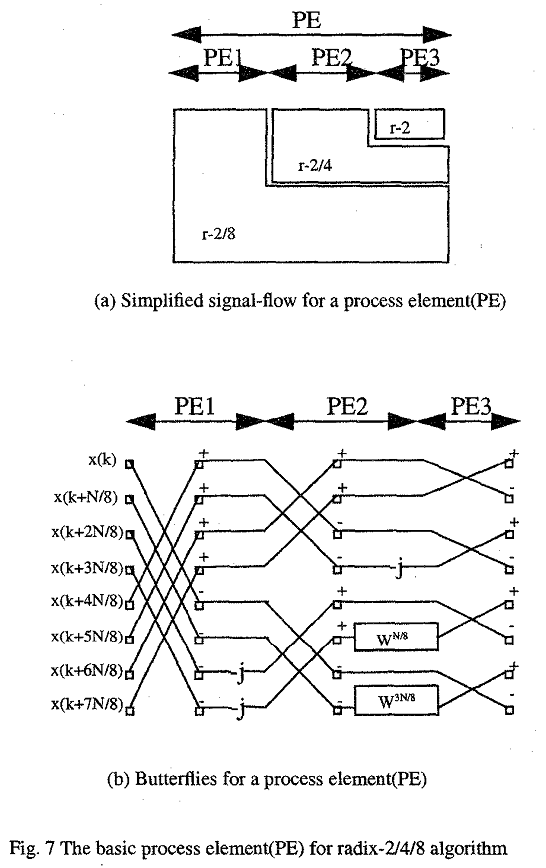
2/4/8基底的信號處理流程與架構圖



22基底


基底的選擇越大會造成蝴蝶形架構更加複雜，控制電路也會複雜化。因此Shousheng He和Mats Torkelson在1996提出了一個2^2基底的FFT演算法，利用旋轉因子的特性：WN4=−j{displaystyle W_{frac {N}{4}}=-j}W_{frac {N}{4}}=-j。而–j的乘法基本上只需要將被乘數的實部虛部對調，然後將虛部加上負號即可，這樣的負數乘法被定義為'簡單乘法'，因此可以用很簡單的硬體架構來實現。利用上面的特性，22基底FFT能用串接的方式將旋轉因子以4為單位對DFT公式進行拆解，將蝴蝶形架構層數降到log4N，大幅減少複數乘法器的用量，而同時卻維持了2基底蝴蝶形架構的簡單性，在效能上獲得改進。22基底DIF FFT演算法的拆解方法如下列公式所述：


N點DFT公式：
X(k)=∑n=0N−1x(n)WNnk,0≦k<N{displaystyle X(k)=sum _{n=0}^{N-1}x(n)W_{N}^{nk},0leqq k<N}X(k)=sum _{n=0}^{N-1}x(n)W_{N}^{nk},0leqq k<N


利用線性映射將n與k映射到三個維度上面


{n=<N2n1+N4n2+n3>Nk=<k1+2k2+4k3>N{displaystyle {begin{cases}n=<{frac {N}{2}}n_{1}+{frac {N}{4}}n_{2}+n_{3}>_{N}\k=<k_{1}+2k_{2}+4k_{3}>_{N}end{cases}}}{begin{cases}n=<{frac {N}{2}}n_{1}+{frac {N}{4}}n_{2}+n_{3}>_{N}\k=<k_{1}+2k_{2}+4k_{3}>_{N}end{cases}}


然後套用Common Factor Algorithm（CFA）


X(k1+2k2+4k3)=∑n3=0N4−1∑n2=01∑n1=01x(N2n1+N4n2+n3)WN(N2n1+N4n2+n3)(k1+2k2+4k3){displaystyle X(k_{1}+2k_{2}+4k_{3})=sum _{n_{3}=0}^{{frac {N}{4}}-1}sum _{n_{2}=0}^{1}sum _{n_{1}=0}^{1}x({frac {N}{2}}n_{1}+{frac {N}{4}}n_{2}+n_{3})W_{N}^{({frac {N}{2}}n_{1}+{frac {N}{4}}n_{2}+n_{3})(k_{1}+2k_{2}+4k_{3})}}X(k_{1}+2k_{2}+4k_{3})=sum _{n_{3}=0}^{{frac {N}{4}}-1}sum _{n_{2}=0}^{1}sum _{n_{1}=0}^{1}x({frac {N}{2}}n_{1}+{frac {N}{4}}n_{2}+n_{3})W_{N}^{({frac {N}{2}}n_{1}+{frac {N}{4}}n_{2}+n_{3})(k_{1}+2k_{2}+4k_{3})}


=∑n3=0N4−1∑n2=01{BN2k1WN(N4n2+n3)k1}WN(N4n2+n3)(2k2+4k3){displaystyle =sum _{n_{3}=0}^{{frac {N}{4}}-1}sum _{n_{2}=0}^{1}{begin{Bmatrix}B_{frac {N}{2}}^{k_{1}}W_{N}^{({frac {N}{4}}n_{2}+n_{3})k_{1}}end{Bmatrix}}W_{N}^{({frac {N}{4}}n_{2}+n_{3})(2k_{2}+4k_{3})}}=sum _{n_{3}=0}^{{frac {N}{4}}-1}sum _{n_{2}=0}^{1}{begin{Bmatrix}B_{frac {N}{2}}^{k_{1}}W_{N}^{({frac {N}{4}}n_{2}+n_{3})k_{1}}end{Bmatrix}}W_{N}^{({frac {N}{4}}n_{2}+n_{3})(2k_{2}+4k_{3})}


而蝴蝶型架構會變成以下形式


BN2k1=x(N4n2+n3)+(−1)k1x(N4n2+n3+N2){displaystyle B_{frac {N}{2}}^{k_{1}}=x({frac {N}{4}}n_{2}+n_{3})+(-1)^{k_{1}}x({frac {N}{4}}n_{2}+n_{3}+{frac {N}{2}})}B_{frac {N}{2}}^{k_{1}}=x({frac {N}{4}}n_{2}+n_{3})+(-1)^{k_{1}}x({frac {N}{4}}n_{2}+n_{3}+{frac {N}{2}})


利用旋轉因子WN4=−j{displaystyle W_{frac {N}{4}}=-j}W_{frac {N}{4}}=-j的特性，可以觀察出


WN(N4n2+n3)(k1+2k2+4k3)=WNNn2n3WNN4n2(k1+2k2)WNn3(k1+2k2)WN4n3k3{displaystyle W_{N}^{({frac {N}{4}}n_{2}+n_{3})(k_{1}+2k_{2}+4k_{3})}=W_{N}^{Nn_{2}n_{3}}W_{N}^{{frac {N}{4}}n_{2}(k_{1}+2k_{2})}W_{N}^{n_{3}(k_{1}+2k_{2})}W_{N}^{4n_{3}k_{3}}}W_{N}^{({frac {N}{4}}n_{2}+n_{3})(k_{1}+2k_{2}+4k_{3})}=W_{N}^{Nn_{2}n_{3}}W_{N}^{{frac {N}{4}}n_{2}(k_{1}+2k_{2})}W_{N}^{n_{3}(k_{1}+2k_{2})}W_{N}^{4n_{3}k_{3}}


=(−j)n2(k1+2k2)WNn3(k1+2k2)WN4n3k3{displaystyle =(-j)^{n_{2}(k_{1}+2k_{2})}W_{N}^{n_{3}(k_{1}+2k_{2})}W_{N}^{4n_{3}k_{3}}}=(-j)^{n_{2}(k_{1}+2k_{2})}W_{N}^{n_{3}(k_{1}+2k_{2})}W_{N}^{4n_{3}k_{3}}


再將此公式帶入原式中可以得到


X(k1+2k2+4k3)=∑n3=0N4−1[H(k1,k2,n3)WNn3(k1+2k2)]WN4n3k3{displaystyle X(k_{1}+2k_{2}+4k_{3})=sum _{n_{3}=0}^{{frac {N}{4}}-1}[H(k_{1},k_{2},n_{3})W_{N}^{n_{3}(k_{1}+2k_{2})}]W_{N}^{4n_{3}k_{3}}}X(k_{1}+2k_{2}+4k_{3})=sum _{n_{3}=0}^{{frac {N}{4}}-1}[H(k_{1},k_{2},n_{3})W_{N}^{n_{3}(k_{1}+2k_{2})}]W_{N}^{4n_{3}k_{3}}


H(k1,k2,n3)=BF2I[x(n3)+(−1)k1(n3+N2)]⏞+(−j)k1+2k2BF2I[x(n3+N4)+(−1)k1(n3+3N4)]⏞⏟BF2II{displaystyle H(k_{1},k_{2},n_{3})={begin{matrix}underbrace {{begin{matrix}BF2I\overbrace {[x(n_{3})+(-1)^{k_{1}}(n_{3}+{frac {N}{2}})]} end{matrix}}{begin{matrix}\\+(-j)^{k_{1}+2k_{2}}end{matrix}}{begin{matrix}BF2I\overbrace {[x(n_{3}+{frac {N}{4}})+(-1)^{k_{1}}(n_{3}+{frac {3N}{4}})]} end{matrix}}} \BF2IIend{matrix}}}H(k_{1},k_{2},n_{3})={begin{matrix}underbrace {{begin{matrix}BF2I\overbrace {[x(n_{3})+(-1)^{k_{1}}(n_{3}+{frac {N}{2}})]} end{matrix}}{begin{matrix}\\+(-j)^{k_{1}+2k_{2}}end{matrix}}{begin{matrix}BF2I\overbrace {[x(n_{3}+{frac {N}{4}})+(-1)^{k_{1}}(n_{3}+{frac {3N}{4}})]} end{matrix}}} \BF2IIend{matrix}}


如上述公式所示，原本的DFT公式會被拆解成多個H(k1,k2,n3){displaystyle H(k_{1},k_{2},n_{3})}H(k_{1},k_{2},n_{3})，而H(k1,k2,n3){displaystyle H(k_{1},k_{2},n_{3})}H(k_{1},k_{2},n_{3})又可分為BF2I與BF2II兩個階層，分別會對應到之後所介紹的兩種硬體架構。


一個16點的DFT公式經過一次上面所述之拆解之後可得下面的FFT架構


Radix-22 16point.png


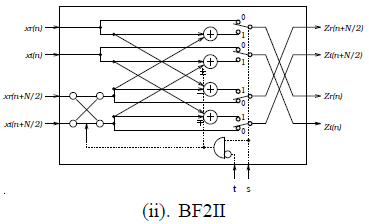
可以看出上圖的架構保留了2基底的簡單架構，然而複數乘法卻降到每兩級才出現一次，也就是log4N{displaystyle log_{4}N}log_{4}N次。而BF2I以及BF2II所對應的硬體架構下圖：


BF2 IBF2 II


其中BF2II硬體單元中左下角的交叉電路就是用來處理-j的乘法。


一個256點的FFT架構可以由下面的硬體來實現：


Radix22-128point.png


其中圖下方的為一7位元寬的計數器，而此架構的控制電路相當單純，只要將計數器的各個位元分別接上BF2I與BF2II單元即可。


下表將2基底、4基底與22基底演算法做一比較，可以發現22基底演算法所需要的乘法氣數量為2基底的一半，加法棄用量是4基底的一半，並維持一樣的記憶體用量和控制電路的簡單性。


































乘法器與加法器數量比較
乘法數 加法數 記憶體大小 控制電路
R2SDF
 2(log4N-1) 4log4N N-1 簡單
R4SDF
 log4N -1 8log4N N-1 中等
R22SDF
 log4N -1 4log4N N-1 簡單


23基底


如上所述，22演算法是將旋轉因子WN4=−j{displaystyle W^{frac {N}{4}}=-j}W^{frac {N}{4}}=-j視為一個簡單乘法，進而由公式以及硬體上的化簡獲得硬體需求上的改進。而藉由相同的概念，Shousheng He和Mats Torkelson進一步將旋轉因子WN8=22(1−j){displaystyle W^{frac {N}{8}}={frac {sqrt {2}}{2}}(1-j)}W^{frac {N}{8}}={frac {sqrt {2}}{2}}(1-j)的乘法化簡成一個簡單乘法，而化簡的方法將會在下面講解。



22{displaystyle {frac {sqrt {2}}{2}}}{frac {sqrt {2}}{2}}乘法化簡


在2基數FFT演算法中的基本概念是利用旋轉因子Wnk,WN2{displaystyle W^{nk},W^{frac {N}{2}}}W^{nk},W^{frac {N}{2}}的對稱性，4基數演算法則是利用
Wnk+N4=−Wnk+3N4=−jWnk{displaystyle W^{nk+{frac {N}{4}}}=-W^{nk+{frac {3N}{4}}}=-jW^{nk}}W^{nk+{frac {N}{4}}}=-W^{nk+{frac {3N}{4}}}=-jW^{nk}
的特性。但是我們會發現在這些旋轉因子的對稱特性中─


WN8=−W5N8=22(1−j),W3N8=−W7N8=−22(1+j){displaystyle W^{frac {N}{8}}=-W^{frac {5N}{8}}={frac {sqrt {2}}{2}}(1-j),W^{frac {3N}{8}}=-W^{frac {7N}{8}}=-{frac {sqrt {2}}{2}}(1+j)}W^{frac {N}{8}}=-W^{frac {5N}{8}}={frac {sqrt {2}}{2}}(1-j),W^{frac {3N}{8}}=-W^{frac {7N}{8}}=-{frac {sqrt {2}}{2}}(1+j)


─並沒有被利用到。主要是因為22(1−j){displaystyle {frac {sqrt {2}}{2}}(1-j)}{frac {sqrt {2}}{2}}(1-j)的乘法運算會讓整個FFT變得複雜，但是如果藉由近似的方法，我們便可以將此一運算化簡為12個加法。


22=0.70710678=2−1+2−3+2−4+2−6+2−8+2−9{displaystyle {frac {sqrt {2}}{2}}=0.70710678=2^{-1}+2^{-3}+2^{-4}+2^{-6}+2^{-8}+2^{-9}}{frac {sqrt {2}}{2}}=0.70710678=2^{-1}+2^{-3}+2^{-4}+2^{-6}+2^{-8}+2^{-9}


我們可以從上式注意到，22{displaystyle {frac {sqrt {2}}{2}}}{frac {sqrt {2}}{2}}可以被近似為五個加法的結果，所以22(1+j){displaystyle {frac {sqrt {2}}{2}}(1+j)}{frac {sqrt {2}}{2}}(1+j)就可以被簡化為只有六個加法，再算入實部與虛部的計算，總共只需12個加法器就可以運用到此一簡化特性。


12adder multi.png


經由與22基底類似的推導，並用串接的方式將旋轉因子以8為單位對DFT公式進行拆解，23基底FFT演算法進一步將複數乘法器的用量縮減到log8N，並同時維持硬體架構的簡單性。
　　
推導的方法與22基底相當類似。藉由這樣的方法，23基底能將乘法器的用量縮減到2基底的1/3，並同時維持一樣的記憶體用量以及控制電路的簡單性。



參考資料





  1. ^ 程佩青. 数字信号处理教程. 清华大学出版社. 2001. ISBN 9787900631671. 




  1. Widhe, T., J. Melander, et al. (1997). Design of efficient radix-8 butterfly PEs for VLSI. Circuits and Systems, 1997. ISCAS '97., Proceedings of 1997 IEEE International Symposium on.

  2. Lihong, J., G. Yonghong, et al. (1998). A new VLSI-oriented FFT algorithm and implementation. ASIC Conference 1998. Proceedings. Eleventh Annual IEEE International.

  3. Duhamel, P. and H. Hollmann (1984). "Split-radix FFT algorithm." Electronics Letters 20(1): 14-16.

  4. Vetterli, M. and P. Duhamel (1989). "Split-radix algorithms for length-pm DFT's." Acoustics, Speech and Signal Processing, IEEE Transactions on 37(1): 57-64.

  5. Richards, M. A. (1988). "On hardware implementation of the split-radix FFT." Acoustics, Speech and Signal Processing, IEEE Transactions on 36(10): 1575-1581.

  6. Shousheng, H. and M. Torkelson (1996). A new approach to pipeline FFT processor. Parallel Processing Symposium, 1996., Proceedings of IPPS '96, The 10th International.

  7. Shousheng, H. and M. Torkelson (1998). Designing pipeline FFT processor for OFDM (de)modulation. Signals, Systems, and Electronics, 1998. ISSSE 98. 1998 URSI International Symposium on.




-

Popular posts from this blog

Y

Image
This article is about the letter of the alphabet. For other uses, see Y (disambiguation). See also: Wye (disambiguation) Y Y y (See below) Usage Writing system Latin script Type Alphabetic and Logographic Language of origin Latin language Phonetic usage [ y ] [ ɨ ] [ j ] [ iː ] [ ɪ ] [ ɘ ] [ ə ] [ ɯ ] [ ɛː ] [ j ] [ ɥ ] [ ɣ̟ ] / w aɪ / / aɪ / Unicode value U+0059, U+0079 Alphabetical position 25 History Development Υ υ 𐌖 Y y Time period 54 to present Descendants  • U  • V  • W  • Ỿ  • ¥  • Ꮙ  • Ꮍ  • Ꭹ Sisters F Ѵ У Ў Ұ Ү ו و ܘ וּ וֹ ࠅ 𐎆 𐡅 ወ વ ૂ ુ उ Variations (See below) Other Other letters commonly used with y(x), ly, ny This article contains IPA phonetic symbols. Without proper rendering support, you may see question marks, boxes, or other symbols instead of Unicode characters. For an introductory guide on IPA symbols, see Help:IPA. ISO basic Latin alphabet Aa Bb Cc D...
Read more

Mount Tamalpais

Image
Mount Tamalpais Mount Tamalpais, viewed from the south Highest point Elevation 2,571 ft (784 m)   NAVD 88 [1] Prominence 2,456 ft (749 m)  [1] Listing California county high points 55th Coordinates 37°55′45″N 122°34′40″W  /  37.929088°N 122.577829°W  / 37.929088; -122.577829 Coordinates: 37°55′45″N 122°34′40″W  /  37.929088°N 122.577829°W  / 37.929088; -122.577829   [1] Geography Mount Tamalpais Marin County, California, U.S. Show map of California Mount Tamalpais Mount Tamalpais (the US) Show map of the US Parent range California Coast Ranges Topo map USGS San Rafael Geology Mountain type Sedimentary Climbing First ascent 1830s by Jacob P. Leese (first recorded ascent) [2] Easiest route Railroad Grade fire trail Mount Tamalpais ( / t æ m əl ˈ p aɪ . ɪ s / ; TAM -əl- PY -iss ; Coast Miwok: /t̪ɑmɑlˈpɑis̺/ , known locally as Mount Tam ) is a peak in Marin County, California, United State...
Read more

Indian Forest Service

Image
Indian Forest Service Service Overview Preceding service Imperial Forest Service (1864 to 1935) Year of Constitution 1966 Country India Staff College Indira Gandhi National Forest Academy (IGNFA), Dehradun, Uttarakhand Cadre Controlling Authority Ministry of Environment, Forests and Climate Change Legal personality Governmental: Government service General nature Administration of Forest and Wildlife resources Cadre strength 3131 (2182 Direct Recruits and 949 Promotion Posts) Website ifs.nic.in Service Chief Director General of Forests Siddhanth Das, IFS (1982 Batch, Odisha Cadre) [1] Head of the All India Civil Services Cabinet Secretary Pradeep Kumar Sinha, IAS Indian Forest Service (भारतीय वन सेवा) [2] is one of the three All India Services of the Government of India. The other two All India Services being the Indian Administrative Service (IAS) and the Indian Police Service (IPS). [3] [4] [5] It was constituted in...
Read more