耦合常數
在物理学中,耦合常數决定了相互作用的強度。例如在牛顿万有引力定律和爱因斯坦的广义相对论中,牛顿常数 GN{displaystyle G_{N}}

其中ge{displaystyle g_{e}}

在拉格朗日系统中,拉格朗日量或哈密顿量可以分成动能部分和相互作用部分。耦合常数决定了决定了相互作用部分相对于动能部分的强度。在存在多种相互作用的情况下,耦合常数也决定着各个相互作用的相对强度。
在经典力学中,耦合常数的大小可以通过测量力的大小直接得到。历史上牛顿常数是在牛顿死后71年后才由卡文迪什通过扭秤实验测量得到。但在量子力学中由于量子涨落的存在,出现在拉格朗日量或哈密顿量中的耦合常数是无法直接通过测量得到的。而实验中测量得到的耦合常数会随着探测尺度的不同而不同,被称为跑动的耦合常数。相应的,拉格朗日量中的耦合常数被称为裸耦合常数。
如果一个物理系统的相互作用的耦合常数比较小,则它的解可以通过微扰论近似得到。微扰论在量子场论的计算中尤其重要。
目录
1 基本相互作用
2 弱耦合与微扰论
3 跑动的耦合常数
3.1 量子电动力学和朗道奇點
3.2 量子色动力学和漸近自由
4 弦理論
5 相關條目
6 參考資料
基本相互作用
强、弱、电磁和引力四种基本相互作用中的耦合常数的大小大致如下
[1]:
| 相互作用 | 耦合常数 |
|---|---|
| 强相互作用 | gs≃1.214{displaystyle g_{s}simeq 1.214}  |
| 电磁相互作用 | ge≃0.302822{displaystyle g_{e}simeq 0.302822}  |
| 弱相互作用 | gW≃0.6295,gZ≃0.7180{displaystyle g_{W}simeq 0.6295,quad g_{Z}simeq 0.7180}  |
| 引力相互作用 | GN≃6.674×10−11m3kg−1s−2{displaystyle G_{N}simeq 6.674times 10^{-11}mathrm {m^{3}kg^{-1}s^{-2}} }  |
弱耦合与微扰论
如果一个问题中的耦合常数g{displaystyle g}


- A=A0+gA1+g2A2+...{displaystyle A=A_{0}+gA_{1}+g^{2}A_{2}+...}
- A=A0+gA1+g2A2+...{displaystyle A=A_{0}+gA_{1}+g^{2}A_{2}+...}
其中,A0{displaystyle A_{0}}

微扰论在量子场论中具有核心地位。量子场论中的微扰论计算一般是通过费曼图和费曼规则来系统地组织实现的,因为费曼图就是按照耦合常数的幂次画出来的。电磁相互作用、弱相互作用在寻常尺度下都是弱耦合的相互作用。而强相互作用在短距离上(尺度远小于飞米时)也是弱耦合的。
跑动的耦合常数
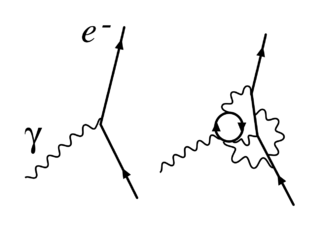
在量子力学尤其是量子场论中,由于量子涨落效应的存在,相互作用顶点被虚粒子所修正,成为非定域性的相互作用顶点。因此,测得的耦合常数的大小与原拉格朗日量或哈密顿量中的裸耦合常数不同,且与测量的能量标度有关。后一点可以通过不确定关系,ΔpΔx≥12ℏ{displaystyle Delta pDelta xgeq {frac {1}{2}}hbar }
β函數β(g) 描述了耦合常数随能量标度μ變化的的情形,其定義如下
- β(g)=μ∂g∂μ=∂g∂lnμ,{displaystyle beta (g)=mu {frac {partial g}{partial mu }}={frac {partial g}{partial ln mu }},}
- β(g)=μ∂g∂μ=∂g∂lnμ,{displaystyle beta (g)=mu {frac {partial g}{partial mu }}={frac {partial g}{partial ln mu }},}
其中μ為特定物理过程的能量标度。
若量子场论中的β函數為零,則此理論為共形場論。若在高能量下β函数为正,代表耦合常数随着能标的增加而增加;若在高能量下β函数为负,则代表耦合常数随着能标的增加减小,这种现象叫做漸近自由。
量子电动力学和朗道奇點
根据微扰论,描写电磁相互作用的量子电动力学的β函數为正,耦合效應會隨著能量增加而增強。量子电动力学在高能量時會變得高度耦合,甚至在某些有限時能量下,耦合係數似乎會變成無限大,此現象最早是由列夫·达维多维奇·郎道所發現,因此稱為郎道奇點。不過微擾论在强耦合情况下已经失效。而且达到朗道奇点所需的能标远远超过普朗克能标,而一般认为量子场论在普朗克能标左右已经不再适用。
量子色动力学和漸近自由

精确到gs2{displaystyle g_{s}^{2}}
 阶的强相互作用的耦合常数随着能标的变化
阶的强相互作用的耦合常数随着能标的变化弗朗克·韦尔切克、休·波利策及戴维·格娄斯發現,描写强相互作用的量子色动力学的β函數為负。因此量子色动力学的耦合在高能量時會降低。其發現者因此获得2004年的諾貝爾物理獎[2]。在一阶近似下耦合係數大致可以表示為下式:
- αs(μ2) =def gs2(μ2)4π≈1β0ln(μ2/Λ2),{displaystyle alpha _{s}(mu ^{2}) {stackrel {mathrm {def} }{=}} {frac {g_{s}^{2}(mu ^{2})}{4pi }}approx {frac {1}{beta _{0}ln(mu ^{2}/Lambda ^{2})}},}
- αs(μ2) =def gs2(μ2)4π≈1β0ln(μ2/Λ2),{displaystyle alpha _{s}(mu ^{2}) {stackrel {mathrm {def} }{=}} {frac {g_{s}^{2}(mu ^{2})}{4pi }}approx {frac {1}{beta _{0}ln(mu ^{2}/Lambda ^{2})}},}
其中β0=112π(33−2Nf){displaystyle beta _{0}={frac {1}{12pi }}(33-2N_{f})}

相反的,耦合程度會隨著能量降低而增強,因此在低能量時耦合效應會變強。尤其是在能标Λ上由微扰论定义耦合常数开始出现发散,因此不能用微擾效應來求解。Λ稱為QCD尺度,其數值為
- ΛMS=217−23+25 MeV{displaystyle Lambda _{MS}=217_{-23}^{+25}{rm { MeV}}}
- ΛMS=217−23+25 MeV{displaystyle Lambda _{MS}=217_{-23}^{+25}{rm { MeV}}}
大致对应于一飞米。
弦理論
弦理論下的耦合常數有明顯的不同點,弦耦合常數一方面意味著決定一根弦分裂的能力,另一方面則意味著弦理論的每一個微擾敘述和一個弦耦合常數有關,可是這些耦合常數不是事先定義、可調整及共適性的常數,而是動態的純量場,會依位置和時間改善,而其數值需動態決定。
相關條目
- 耦合 (物理學)
量子场论、量子電動力學及量子色動力學
规范量子化、重整化及维度正则化
- 精细结构常数
- 重力耦合常數
- 費米耦合常數
參考資料
^ Griffiths, David. Introduction to Elementary Particles 2nd, Revised. KGaA, Weinheim: Wiley-VCH Verlag GmbH & Co. 2008: XVI. ISBN :978-3-527-40601-2 请检查|isbn=值 (帮助).
^ The Nobel Prize in Physics 2004. NobelPrize.org. Nobel Media. [2011-08-26].
| |||||||||||||||||||||||||||||||||||||




