Brstjjy

Part of a series of articles about
Classical mechanics
F→=ma→{displaystyle {vec {F}}=m{vec {a}}} Second law of motion
History Timeline
Branches Applied Celestial Continuum Dynamics Kinematics Kinetics Statics Statistical
Fundamentals Acceleration Angular momentum Couple D'Alembert's principle Energy kinetic potential Force Frame of reference Inertial frame of reference Impulse Inertia / Moment of inertia Mass Mechanical power Mechanical work Moment Momentum Space Speed Time Torque Velocity Virtual work
Formulations Newton's laws of motion Analytical mechanics Lagrangian mechanics Hamiltonian mechanics Routhian mechanics Hamilton–Jacobi equation Appell's equation of motion Udwadia–Kalaba equation Koopman–von Neumann mechanics
Core topics Damping (ratio) Displacement Equations of motion Euler's laws of motion Fictitious force Friction Harmonic oscillator Inertial / Non-inertial reference frame Mechanics of planar particle motion Motion (linear) Newton's law of universal gravitation Newton's laws of motion Relative velocity Rigid body dynamics Euler's equations Simple harmonic motion Vibration
Rotation Circular motion Rotating reference frame Centripetal force Centrifugal force reactive Coriolis force Pendulum Tangential speed Rotational speed Angular acceleration / displacement / frequency / velocity
Scientists Galileo Huygens Newton Kepler Horrocks Halley Euler d'Alembert Clairaut Lagrange Laplace Hamilton Poisson Daniel Bernoulli Johann Bernoulli Cauchy
v t e

A centripetal force (from Latin centrum, "center" and petere, "to seek"^[1]) is a force that makes a body follow a curved path. Its direction is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre".^[2] In Newtonian mechanics, gravity provides the centripetal force responsible for astronomical orbits.

One common example involving centripetal force is the case in which a body moves with uniform speed along a circular path. The centripetal force is directed at right angles to the motion and also along the radius towards the centre of the circular path.^[3][4] The mathematical description was derived in 1659 by the Dutch physicist Christiaan Huygens.^[5]

Formula

The magnitude of the centripetal force on an object of mass m moving at tangential speed v along a path with radius of curvature r is:^[6]

F=mac=mv2r{displaystyle F=ma_{c}={frac {mv^{2}}{r}}}

where ac{displaystyle a_{c}} is the centripetal acceleration.
The direction of the force is toward the center of the circle in which the object is moving, or the osculating circle (the circle that best fits the local path of the object, if the path is not circular).^[7]
The speed in the formula is squared, so twice the speed needs four times the force. The inverse relationship with the radius of curvature shows that half the radial distance requires twice the force. This force is also sometimes written in terms of the angular velocity ω of the object about the center of the circle, related to the tangential velocity by the formula

v=ωr{displaystyle v=omega r}

so that

F=mrω2.{displaystyle F=mromega ^{2},.}

Expressed using the orbital period T for one revolution of the circle,

ω=2πT{displaystyle omega ={frac {2pi }{T}},}

the equation becomes

F=mr(2πT)2.{displaystyle F=mrleft({frac {2pi }{T}}right)^{2}.}^[8]

In particle accelerators, velocity can be very high (close to the speed of light in vacuum) so the same rest mass now exerts greater inertia (relativistic mass) thereby requiring greater force for the same centripetal acceleration, so the equation becomes:

F=γmv2r{displaystyle F={frac {gamma mv^{2}}{r}}}

where

γ=11−v2/c2{displaystyle gamma ={frac {1}{sqrt {1-v^{2}/c^{2}}}}}

is called the Lorentz factor.

More intuitively:

F=γmvω{displaystyle F=gamma mvomega }

which is the rate of change of relativistic momentum (γmv{displaystyle gamma mv})

Sources

A body experiencing uniform circular motion requires a centripetal force, towards the axis as shown, to maintain its circular path.

In the case of an object that is swinging around on the end of a rope in a horizontal plane, the centripetal force on the object is supplied by the tension of the rope. The rope example is an example involving a 'pull' force. The centripetal force can also be supplied as a 'push' force, such as in the case where the normal reaction of a wall supplies the centripetal force for a wall of death rider.

Newton's idea of a centripetal force corresponds to what is nowadays referred to as a central force. When a satellite is in orbit around a planet, gravity is considered to be a centripetal force even though in the case of eccentric orbits, the gravitational force is directed towards the focus, and not towards the instantaneous center of curvature.^[9]

Another example of centripetal force arises in the helix that is traced out when a charged particle moves in a uniform magnetic field in the absence of other external forces. In this case, the magnetic force is the centripetal force that acts towards the helix axis.

Analysis of several cases

Below are three examples of increasing complexity, with derivations of the formulas governing velocity and acceleration.

Uniform circular motion

Uniform circular motion refers to the case of constant rate of rotation. Here are two approaches to describing this case.

Calculus derivation

In two dimensions, the position vector r{displaystyle {textbf {r}}}, which has magnitude (length) r{displaystyle r} and directed at an angle θ{displaystyle theta } above the x-axis, can be expressed in Cartesian coordinates using the unit vectors x^{displaystyle {hat {x}}} and y^{displaystyle {hat {y}}}:^[10]

r=rcos⁡(θ)x^+rsin⁡(θ)y^.{displaystyle {textbf {r}}=rcos(theta ){hat {x}}+rsin(theta ){hat {y}}.}

Assume uniform circular motion, which requires three things.

1. The object moves only on a circle.


2. The radius of the circle r{displaystyle r} does not change in time.


3. The object moves with constant angular velocity ω{displaystyle omega } around the circle. Therefore, θ=ωt{displaystyle theta =omega t} where t{displaystyle t} is time.

Now find the velocity v{displaystyle {textbf {v}}} and acceleration a{displaystyle {textbf {a}}} of the motion by taking derivatives of position with respect to time.

r=rcos⁡(ωt)x^+rsin⁡(ωt)y^{displaystyle {textbf {r}}=rcos(omega t){hat {x}}+rsin(omega t){hat {y}}}

r˙=v=−rωsin⁡(ωt)x^+rωcos⁡(ωt)y^{displaystyle {dot {textbf {r}}}={textbf {v}}=-romega sin(omega t){hat {x}}+romega cos(omega t){hat {y}}}

r¨=a=−rω2cos⁡(ωt)x^−rω2sin⁡(ωt)y^{displaystyle {ddot {textbf {r}}}={textbf {a}}=-romega ^{2}cos(omega t){hat {x}}-romega ^{2}sin(omega t){hat {y}}}

a=−ω2(rcos⁡(ωt)x^+rsin⁡(ωt)y^){displaystyle {textbf {a}}=-omega ^{2}(rcos(omega t){hat {x}}+rsin(omega t){hat {y}})}

Notice that the term in parenthesis is the original expression of r{displaystyle {textbf {r}}} in Cartesian coordinates. Consequently,

a=−ω2r.{displaystyle {textbf {a}}=-omega ^{2}{textbf {r}}.}

negative shows that the acceleration is pointed towards the center of the circle (opposite the radius), hence it is called "centripetal" (i.e. "center-seeking"). While objects naturally follow a straight path (due to inertia), this centripetal acceleration describes the circular motion path caused by a centripetal force.

Derivation using vectors

Vector relationships for uniform circular motion; vector Ω representing the rotation is normal to the plane of the orbit with polarity determined by the right-hand rule and magnitude dθ /dt.

The image at right shows the vector relationships for uniform circular motion. The rotation itself is represented by the angular velocity vector Ω, which is normal to the plane of the orbit (using the right-hand rule) and has magnitude given by:

|Ω|=dθdt=ω ,{displaystyle |mathbf {Omega } |={frac {mathrm {d} theta }{mathrm {d} t}}=omega ,}

with θ the angular position at time t. In this subsection, dθ/dt is assumed constant, independent of time. The distance traveled dℓ of the particle in time dt along the circular path is

dℓ=Ω×r(t)dt ,{displaystyle mathrm {d} {boldsymbol {ell }}=mathbf {Omega } times mathbf {r} (t)mathrm {d} t ,}

which, by properties of the vector cross product, has magnitude rdθ and is in the direction tangent to the circular path.

Consequently,

drdt=limΔt→0r(t+Δt)−r(t)Δt=dℓdt .{displaystyle {frac {mathrm {d} mathbf {r} }{mathrm {d} t}}=lim _{{Delta }tto 0}{frac {mathbf {r} (t+{Delta }t)-mathbf {r} (t)}{{Delta }t}}={frac {mathrm {d} {boldsymbol {ell }}}{mathrm {d} t}} .}

In other words,

v =def drdt=dℓdt=Ω×r(t) .{displaystyle mathbf {v} {stackrel {mathrm {def} }{=}} {frac {mathrm {d} mathbf {r} }{mathrm {d} t}}={frac {mathrm {d} mathbf {boldsymbol {ell }} }{mathrm {d} t}}=mathbf {Omega } times mathbf {r} (t) .}

Differentiating with respect to time,

a =def dvdt=Ω×dr(t)dt=Ω×[Ω×r(t)] .{displaystyle mathbf {a} {stackrel {mathrm {def} }{=}} {frac {mathrm {d} mathbf {v} }{dmathrm {t} }}=mathbf {Omega } times {frac {mathrm {d} mathbf {r} (t)}{mathrm {d} t}}=mathbf {Omega } times left[mathbf {Omega } times mathbf {r} (t)right] .}

Lagrange's formula states:

a×(b×c)=b(a⋅c)−c(a⋅b) .{displaystyle mathbf {a} times left(mathbf {b} times mathbf {c} right)=mathbf {b} left(mathbf {a} cdot mathbf {c} right)-mathbf {c} left(mathbf {a} cdot mathbf {b} right) .}

Applying Lagrange's formula with the observation that Ω • r(t) = 0 at all times,

a=−|Ω|2r(t) .{displaystyle mathbf {a} =-{|mathbf {Omega |} }^{2}mathbf {r} (t) .}

In words, the acceleration is pointing directly opposite to the radial displacement r at all times, and has a magnitude:

|a|=|r(t)|(dθdt)2=rω2 {displaystyle |mathbf {a} |=|mathbf {r} (t)|left({frac {mathrm {d} theta }{mathrm {d} t}}right)^{2}=r{omega }^{2} }

where vertical bars |...| denote the vector magnitude, which in the case of r(t) is simply the radius r of the path. This result agrees with the previous section, though the notation is slightly different.

When the rate of rotation is made constant in the analysis of nonuniform circular motion, that analysis agrees with this one.

A merit of the vector approach is that it is manifestly independent of any coordinate system.

Example: The banked turn

Upper panel: Ball on a banked circular track moving with constant speed v; Lower panel: Forces on the ball

The upper panel in the image at right shows a ball in circular motion on a banked curve. The curve is banked at an angle θ from the horizontal, and the surface of the road is considered to be slippery. The objective is to find what angle the bank must have so the ball does not slide off the road.^[11] Intuition tells us that, on a flat curve with no banking at all, the ball will simply slide off the road; while with a very steep banking, the ball will slide to the center unless it travels the curve rapidly.

Apart from any acceleration that might occur in the direction of the path, the lower panel of the image above indicates the forces on the ball. There are two forces; one is the force of gravity vertically downward through the center of mass of the ball mg, where m is the mass of the ball and g is the gravitational acceleration; the second is the upward normal force exerted by the road at a right angle to the road surface ma_n. The centripetal force demanded by the curved motion is also shown above. This centripetal force is not a third force applied to the ball, but rather must be provided by the net force on the ball resulting from vector addition of the normal force and the force of gravity. The resultant or net force on the ball found by vector addition of the normal force exerted by the road and vertical force due to gravity must equal the centripetal force dictated by the need to travel a circular path. The curved motion is maintained so long as this net force provides the centripetal force requisite to the motion.

The horizontal net force on the ball is the horizontal component of the force from the road, which has magnitude |F_h| = m|a_n|sinθ. The vertical component of the force from the road must counteract the gravitational force: |F_v| = m|a_n|cosθ = m|g|, which implies |a_n|=|g| / cosθ. Substituting into the above formula for |F_h| yields a horizontal force to be:

|Fh|=m|g|sin θcos θ=m|g|tan θ .{displaystyle |mathbf {F} _{mathrm {h} }|=m|mathbf {g} |{frac {mathrm {sin} theta }{mathrm {cos} theta }}=m|mathbf {g} |mathrm {tan} theta .}

On the other hand, at velocity |v| on a circular path of radius r, kinematics says that the force needed to turn the ball continuously into the turn is the radially inward centripetal force F_c of magnitude:

|Fc|=m|ac|=m|v|2r .{displaystyle |mathbf {F} _{mathrm {c} }|=m|mathbf {a} _{mathrm {c} }|={frac {m|mathbf {v} |^{2}}{r}} .}

Consequently, the ball is in a stable path when the angle of the road is set to satisfy the condition:

m|g|tan θ=m|v|2r ,{displaystyle m|mathbf {g} |mathrm {tan} theta ={frac {m|mathbf {v} |^{2}}{r}} ,}

or,

tan θ=|v|2|g|r .{displaystyle mathrm {tan} theta ={frac {|mathbf {v} |^{2}}{|mathbf {g} |r}} .}

As the angle of bank θ approaches 90°, the tangent function approaches infinity, allowing larger values for |v|²/r. In words, this equation states that for faster speeds (bigger |v|) the road must be banked more steeply (a larger value for θ), and for sharper turns (smaller r) the road also must be banked more steeply, which accords with intuition. When the angle θ does not satisfy the above condition, the horizontal component of force exerted by the road does not provide the correct centripetal force, and an additional frictional force tangential to the road surface is called upon to provide the difference. If friction cannot do this (that is, the coefficient of friction is exceeded), the ball slides to a different radius where the balance can be realized.^[12][13]

These ideas apply to air flight as well. See the FAA pilot's manual.^[14]

Nonuniform circular motion

Velocity and acceleration for nonuniform circular motion: the velocity vector is tangential to the orbit, but the acceleration vector is not radially inward because of its tangential component a_θ that increases the rate of rotation: dω / dt = | a_θ| / R.

As a generalization of the uniform circular motion case, suppose the angular rate of rotation is not constant. The acceleration now has a tangential component, as shown the image at right. This case is used to demonstrate a derivation strategy based on a polar coordinate system.

Let r(t) be a vector that describes the position of a point mass as a function of time. Since we are assuming circular motion, let r(t) = R·u_r, where R is a constant (the radius of the circle) and u_r is the unit vector pointing from the origin to the point mass. The direction of u_r is described by θ, the angle between the x-axis and the unit vector, measured counterclockwise from the x-axis. The other unit vector for polar coordinates, u_θ is perpendicular to u_r and points in the direction of increasing θ. These polar unit vectors can be expressed in terms of Cartesian unit vectors in the x and y directions, denoted i and j respectively:^[15]

u_r = cosθ i + sinθ j

and

u_θ = -sinθ i + cosθ j.

One can differentiate to find velocity:

v=rdurdt=rddt(cos θ i+sin θ j){displaystyle mathbf {v} =r{frac {mathrm {d} mathbf {u} _{mathrm {r} }}{mathrm {d} t}}=r{frac {mathrm {d} }{mathrm {d} t}}left(mathrm {cos} theta mathbf {i} +mathrm {sin} theta mathbf {j} right)}

=rdθdt(−sin θ i+cos θ j){displaystyle =r{frac {dtheta }{dt}}left(-mathrm {sin} theta mathbf {i} +mathrm {cos} theta mathbf {j} right),}

=rdθdtuθ{displaystyle =r{frac {mathrm {d} theta }{mathrm {d} t}}mathbf {u} _{mathrm {theta } },}

=ωruθ{displaystyle =omega rmathbf {u} _{mathrm {theta } },}

where ω is the angular velocity dθ/dt.

This result for the velocity matches expectations that the velocity should be directed tangentially to the circle, and that the magnitude of the velocity should be rω. Differentiating again, and noting that

duθdt=−dθdtur=−ωur ,{displaystyle {{frac {mathrm {d} mathbf {u} _{mathrm {theta } }}{mathrm {d} t}}=-{frac {mathrm {d} theta }{mathrm {d} t}}mathbf {u} _{mathrm {r} }=-omega mathbf {u} _{mathrm {r} }} ,}

we find that the acceleration, a is:

a=r(dωdtuθ−ω2ur) .{displaystyle mathbf {a} =rleft({frac {mathrm {d} omega }{mathrm {d} t}}mathbf {u} _{mathrm {theta } }-omega ^{2}mathbf {u} _{mathrm {r} }right) .}

Thus, the radial and tangential components of the acceleration are:

ar=−ω2r ur=−|v|2r ur {displaystyle mathbf {a} _{mathrm {r} }=-omega ^{2}r mathbf {u} _{mathrm {r} }=-{frac {|mathbf {v} |^{2}}{r}} mathbf {u} _{mathrm {r} } }   and    aθ=r dωdt uθ=d|v|dt uθ ,{displaystyle mathbf {a} _{mathrm {theta } }=r {frac {mathrm {d} omega }{mathrm {d} t}} mathbf {u} _{mathrm {theta } }={frac {mathrm {d} |mathbf {v} |}{mathrm {d} t}} mathbf {u} _{mathrm {theta } } ,}

where |v| = r ω is the magnitude of the velocity (the speed).

These equations express mathematically that, in the case of an object that moves along a circular path with a changing speed, the acceleration of the body may be decomposed into a perpendicular component that changes the direction of motion (the centripetal acceleration), and a parallel, or tangential component, that changes the speed.

General planar motion

Position vector r, always points radially from the origin.

Velocity vector v, always tangent to the path of motion.

Acceleration vector a, not parallel to the radial motion but offset by the angular and Coriolis accelerations, nor tangent to the path but offset by the centripetal and radial accelerations.

Kinematic vectors in plane polar coordinates. Notice the setup is not restricted to 2d space, but a plane in any higher dimension.

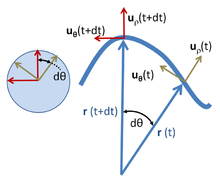
Polar unit vectors at two times t and t + dt for a particle with trajectory r ( t ); on the left the unit vectors u_ρ and u_θ at the two times are moved so their tails all meet, and are shown to trace an arc of a unit radius circle. Their rotation in time dt is dθ, just the same angle as the rotation of the trajectory r ( t ).

Polar coordinates

The above results can be derived perhaps more simply in polar coordinates, and at the same time extended to general motion within a plane, as shown next. Polar coordinates in the plane employ a radial unit vector u_ρ and an angular unit vector u_θ, as shown above.^[16] A particle at position r is described by:

r=ρuρ ,{displaystyle mathbf {r} =rho mathbf {u} _{rho } ,}

where the notation ρ is used to describe the distance of the path from the origin instead of R to emphasize that this distance is not fixed, but varies with time. The unit vector u_ρ travels with the particle and always points in the same direction as r(t). Unit vector u_θ also travels with the particle and stays orthogonal to u_ρ. Thus, u_ρ and u_θ form a local Cartesian coordinate system attached to the particle, and tied to the path traveled by the particle.^[17] By moving the unit vectors so their tails coincide, as seen in the circle at the left of the image above, it is seen that u_ρ and u_θ form a right-angled pair with tips on the unit circle that trace back and forth on the perimeter of this circle with the same angle θ(t) as r(t).

When the particle moves, its velocity is

v=dρdtuρ+ρduρdt .{displaystyle mathbf {v} ={frac {mathrm {d} rho }{mathrm {d} t}}mathbf {u} _{rho }+rho {frac {mathrm {d} mathbf {u} _{rho }}{mathrm {d} t}} .}

To evaluate the velocity, the derivative of the unit vector u_ρ is needed. Because u_ρ is a unit vector, its magnitude is fixed, and it can change only in direction, that is, its change du_ρ has a component only perpendicular to u_ρ. When the trajectory r(t) rotates an amount dθ, u_ρ, which points in the same direction as r(t), also rotates by dθ. See image above. Therefore, the change in u_ρ is

duρ=uθdθ ,{displaystyle mathrm {d} mathbf {u} _{rho }=mathbf {u} _{theta }mathrm {d} theta ,}

or

duρdt=uθdθdt .{displaystyle {frac {mathrm {d} mathbf {u} _{rho }}{mathrm {d} t}}=mathbf {u} _{theta }{frac {mathrm {d} theta }{mathrm {d} t}} .}

In a similar fashion, the rate of change of u_θ is found. As with u_ρ, u_θ is a unit vector and can only rotate without changing size. To remain orthogonal to u_ρ while the trajectory r(t) rotates an amount dθ, u_θ, which is orthogonal to r(t), also rotates by dθ. See image above. Therefore, the change du_θ is orthogonal to u_θ and proportional to dθ (see image above):

duθdt=−dθdtuρ .{displaystyle {frac {mathrm {d} mathbf {u} _{theta }}{mathrm {d} t}}=-{frac {mathrm {d} theta }{mathrm {d} t}}mathbf {u} _{rho } .}

The image above shows the sign to be negative: to maintain orthogonality, if du_ρ is positive with dθ, then du_θ must decrease.

Substituting the derivative of u_ρ into the expression for velocity:

v=dρdtuρ+ρuθdθdt=vρuρ+vθuθ=vρ+vθ .{displaystyle mathbf {v} ={frac {mathrm {d} rho }{mathrm {d} t}}mathbf {u} _{rho }+rho mathbf {u} _{theta }{frac {mathrm {d} theta }{mathrm {d} t}}=v_{rho }mathbf {u} _{rho }+v_{theta }mathbf {u} _{theta }=mathbf {v} _{rho }+mathbf {v} _{theta } .}

To obtain the acceleration, another time differentiation is done:

a=d2ρdt2uρ+dρdtduρdt+dρdtuθdθdt+ρduθdtdθdt+ρuθd2θdt2 .{displaystyle mathbf {a} ={frac {mathrm {d} ^{2}rho }{mathrm {d} t^{2}}}mathbf {u} _{rho }+{frac {mathrm {d} rho }{mathrm {d} t}}{frac {mathrm {d} mathbf {u} _{rho }}{mathrm {d} t}}+{frac {mathrm {d} rho }{mathrm {d} t}}mathbf {u} _{theta }{frac {mathrm {d} theta }{mathrm {d} t}}+rho {frac {mathrm {d} mathbf {u} _{theta }}{mathrm {d} t}}{frac {mathrm {d} theta }{mathrm {d} t}}+rho mathbf {u} _{theta }{frac {mathrm {d} ^{2}theta }{mathrm {d} t^{2}}} .}

Substituting the derivatives of u_ρ and u_θ, the acceleration of the particle is:^[18]

a=d2ρdt2uρ+2dρdtuθdθdt−ρuρ(dθdt)2+ρuθd2θdt2 ,{displaystyle mathbf {a} ={frac {mathrm {d} ^{2}rho }{mathrm {d} t^{2}}}mathbf {u} _{rho }+2{frac {mathrm {d} rho }{mathrm {d} t}}mathbf {u} _{theta }{frac {mathrm {d} theta }{mathrm {d} t}}-rho mathbf {u} _{rho }left({frac {mathrm {d} theta }{mathrm {d} t}}right)^{2}+rho mathbf {u} _{theta }{frac {mathrm {d} ^{2}theta }{mathrm {d} t^{2}}} ,}

=uρ[d2ρdt2−ρ(dθdt)2]+uθ[2dρdtdθdt+ρd2θdt2] {displaystyle =mathbf {u} _{rho }left[{frac {mathrm {d} ^{2}rho }{mathrm {d} t^{2}}}-rho left({frac {mathrm {d} theta }{mathrm {d} t}}right)^{2}right]+mathbf {u} _{theta }left[2{frac {mathrm {d} rho }{mathrm {d} t}}{frac {mathrm {d} theta }{mathrm {d} t}}+rho {frac {mathrm {d} ^{2}theta }{mathrm {d} t^{2}}}right] }

=uρ[dvρdt−vθ2ρ]+uθ[2ρvρvθ+ρddtvθρ] .{displaystyle =mathbf {u} _{rho }left[{frac {mathrm {d} v_{rho }}{mathrm {d} t}}-{frac {v_{theta }^{2}}{rho }}right]+mathbf {u} _{theta }left[{frac {2}{rho }}v_{rho }v_{theta }+rho {frac {mathrm {d} }{mathrm {d} t}}{frac {v_{theta }}{rho }}right] .}

As a particular example, if the particle moves in a circle of constant radius R, then dρ/dt = 0, v = v_θ, and:

a=uρ[−ρ(dθdt)2]+uθ[ρd2θdt2] {displaystyle mathbf {a} =mathbf {u} _{rho }left[-rho left({frac {mathrm {d} theta }{mathrm {d} t}}right)^{2}right]+mathbf {u} _{theta }left[rho {frac {mathrm {d} ^{2}theta }{mathrm {d} t^{2}}}right] }

=uρ[−v2r]+uθ[dvdt] {displaystyle =mathbf {u} _{rho }left[-{frac {v^{2}}{r}}right]+mathbf {u} _{theta }left[{frac {mathrm {d} v}{mathrm {d} t}}right] }

where v=vθ.{displaystyle v=v_{theta }.}

These results agree with those above for nonuniform circular motion. See also the article on non-uniform circular motion. If this acceleration is multiplied by the particle mass, the leading term is the centripetal force and the negative of the second term related to angular acceleration is sometimes called the Euler force.^[19]

For trajectories other than circular motion, for example, the more general trajectory envisioned in the image above, the instantaneous center of rotation and radius of curvature of the trajectory are related only indirectly to the coordinate system defined by u_ρ and u_θ and to the length |r(t)| = ρ. Consequently, in the general case, it is not straightforward to disentangle the centripetal and Euler terms from the above general acceleration equation.^[20][21] To deal directly with this issue, local coordinates are preferable, as discussed next.

Local coordinates

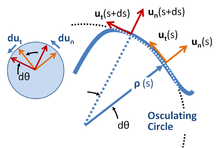
Local coordinate system for planar motion on a curve. Two different positions are shown for distances s and s + ds along the curve. At each position s, unit vector u_n points along the outward normal to the curve and unit vector u_t is tangential to the path. The radius of curvature of the path is ρ as found from the rate of rotation of the tangent to the curve with respect to arc length, and is the radius of the osculating circle at position s. The unit circle on the left shows the rotation of the unit vectors with s.

Local coordinates mean a set of coordinates that travel with the particle,^[22] and have orientation determined by the path of the particle.^[23] Unit vectors are formed as shown in the image at right, both tangential and normal to the path. This coordinate system sometimes is referred to as intrinsic or path coordinates^[24][25] or nt-coordinates, for normal-tangential, referring to these unit vectors. These coordinates are a very special example of a more general concept of local coordinates from the theory of differential forms.^[26]

Distance along the path of the particle is the arc length s, considered to be a known function of time.

s=s(t) .{displaystyle s=s(t) .}

A center of curvature is defined at each position s located a distance ρ (the radius of curvature) from the curve on a line along the normal u_n (s). The required distance ρ(s) at arc length s is defined in terms of the rate of rotation of the tangent to the curve, which in turn is determined by the path itself. If the orientation of the tangent relative to some starting position is θ(s), then ρ(s) is defined by the derivative dθ/ds:

1ρ(s)=κ(s)=dθds .{displaystyle {frac {1}{rho (s)}}=kappa (s)={frac {mathrm {d} theta }{mathrm {d} s}} .}

The radius of curvature usually is taken as positive (that is, as an absolute value), while the curvature κ is a signed quantity.

A geometric approach to finding the center of curvature and the radius of curvature uses a limiting process leading to the osculating circle.^[27][28] See image above.

Using these coordinates, the motion along the path is viewed as a succession of circular paths of ever-changing center, and at each position s constitutes non-uniform circular motion at that position with radius ρ. The local value of the angular rate of rotation then is given by:

ω(s)=dθdt=dθdsdsdt=1ρ(s) dsdt=v(s)ρ(s) ,{displaystyle omega (s)={frac {mathrm {d} theta }{mathrm {d} t}}={frac {mathrm {d} theta }{mathrm {d} s}}{frac {mathrm {d} s}{mathrm {d} t}}={frac {1}{rho (s)}} {frac {mathrm {d} s}{mathrm {d} t}}={frac {v(s)}{rho (s)}} ,}

with the local speed v given by:

v(s)=dsdt .{displaystyle v(s)={frac {mathrm {d} s}{mathrm {d} t}} .}

As for the other examples above, because unit vectors cannot change magnitude, their rate of change is always perpendicular to their direction (see the left-hand insert in the image above):^[29]

dun(s)ds=ut(s)dθds=ut(s)1ρ ;{displaystyle {frac {dmathbf {u} _{mathrm {n} }(s)}{ds}}=mathbf {u} _{mathrm {t} }(s){frac {dtheta }{ds}}=mathbf {u} _{mathrm {t} }(s){frac {1}{rho }} ;} dut(s)ds=−un(s)dθds=−un(s)1ρ .{displaystyle {frac {dmathbf {u} _{mathrm {t} }(s)}{mathrm {d} s}}=-mathbf {u} _{mathrm {n} }(s){frac {mathrm {d} theta }{mathrm {d} s}}=-mathbf {u} _{mathrm {n} }(s){frac {1}{rho }} .}

Consequently, the velocity and acceleration are:^[28][30][31]

v(t)=vut(s) ;{displaystyle mathbf {v} (t)=vmathbf {u} _{mathrm {t} }(s) ;}

and using the chain-rule of differentiation:

a(t)=dvdtut(s)−v2ρun(s) ;{displaystyle mathbf {a} (t)={frac {mathrm {d} v}{mathrm {d} t}}mathbf {u} _{mathrm {t} }(s)-{frac {v^{2}}{rho }}mathbf {u} _{mathrm {n} }(s) ;} with the tangential acceleration dvdt=dvds dsdt=dvds v .{displaystyle {frac {mathrm {mathrm {d} } v}{mathrm {mathrm {d} } t}}={frac {mathrm {d} v}{mathrm {d} s}} {frac {mathrm {d} s}{mathrm {d} t}}={frac {mathrm {d} v}{mathrm {d} s}} v .}

In this local coordinate system, the acceleration resembles the expression for nonuniform circular motion with the local radius ρ(s), and the centripetal acceleration is identified as the second term.^[32]

Extending this approach to three dimensional space curves leads to the Frenet–Serret formulas.^[33][34]

Alternative approach

Looking at the image above, one might wonder whether adequate account has been taken of the difference in curvature between ρ(s) and ρ(s + ds) in computing the arc length as ds = ρ(s)dθ. Reassurance on this point can be found using a more formal approach outlined below. This approach also makes connection with the article on curvature.

To introduce the unit vectors of the local coordinate system, one approach is to begin in Cartesian coordinates and describe the local coordinates in terms of these Cartesian coordinates. In terms of arc length s, let the path be described as:^[35]

r(s)=[x(s), y(s)] .{displaystyle mathbf {r} (s)=left[x(s), y(s)right] .}

Then an incremental displacement along the path ds is described by:

dr(s)=[dx(s), dy(s)]=[x′(s), y′(s)]ds ,{displaystyle mathrm {d} mathbf {r} (s)=left[mathrm {d} x(s), mathrm {d} y(s)right]=left[x'(s), y'(s)right]mathrm {d} s ,}

where primes are introduced to denote derivatives with respect to s. The magnitude of this displacement is ds, showing that:^[36]

[x′(s)2+y′(s)2]=1 .{displaystyle left[x'(s)^{2}+y'(s)^{2}right]=1 .} (Eq. 1)

This displacement is necessarily a tangent to the curve at s, showing that the unit vector tangent to the curve is:

ut(s)=[x′(s), y′(s)] ,{displaystyle mathbf {u} _{mathrm {t} }(s)=left[x'(s), y'(s)right] ,}

while the outward unit vector normal to the curve is

un(s)=[y′(s), −x′(s)] ,{displaystyle mathbf {u} _{mathrm {n} }(s)=left[y'(s), -x'(s)right] ,}

Orthogonality can be verified by showing that the vector dot product is zero. The unit magnitude of these vectors is a consequence of Eq. 1. Using the tangent vector, the angle θ of the tangent to the curve is given by:

sin⁡θ=y′(s)x′(s)2+y′(s)2=y′(s) ;{displaystyle sin theta ={frac {y'(s)}{sqrt {x'(s)^{2}+y'(s)^{2}}}}=y'(s) ;} and cos⁡θ=x′(s)x′(s)2+y′(s)2=x′(s) .{displaystyle cos theta ={frac {x'(s)}{sqrt {x'(s)^{2}+y'(s)^{2}}}}=x'(s) .}

The radius of curvature is introduced completely formally (without need for geometric interpretation) as:

1ρ=dθds .{displaystyle {frac {1}{rho }}={frac {mathrm {d} theta }{mathrm {d} s}} .}

The derivative of θ can be found from that for sinθ:

dsin⁡θds=cos⁡θdθds=1ρcos⁡θ =1ρx′(s) .{displaystyle {frac {mathrm {d} sin theta }{mathrm {d} s}}=cos theta {frac {mathrm {d} theta }{mathrm {d} s}}={frac {1}{rho }}cos theta ={frac {1}{rho }}x'(s) .}

Now:

dsin⁡θds=ddsy′(s)x′(s)2+y′(s)2{displaystyle {frac {mathrm {d} sin theta }{mathrm {d} s}}={frac {mathrm {d} }{mathrm {d} s}}{frac {y'(s)}{sqrt {x'(s)^{2}+y'(s)^{2}}}}} =y″(s)x′(s)2−y′(s)x′(s)x″(s)(x′(s)2+y′(s)2)3/2 ,{displaystyle ={frac {y''(s)x'(s)^{2}-y'(s)x'(s)x''(s)}{left(x'(s)^{2}+y'(s)^{2}right)^{3/2}}} ,}

in which the denominator is unity. With this formula for the derivative of the sine, the radius of curvature becomes:

dθds=1ρ=y″(s)x′(s)−y′(s)x″(s) {displaystyle {frac {mathrm {d} theta }{mathrm {d} s}}={frac {1}{rho }}=y''(s)x'(s)-y'(s)x''(s) } =y″(s)x′(s)=−x″(s)y′(s) ,{displaystyle ={frac {y''(s)}{x'(s)}}=-{frac {x''(s)}{y'(s)}} ,}

where the equivalence of the forms stems from differentiation of Eq. 1:

x′(s)x″(s)+y′(s)y″(s)=0 .{displaystyle x'(s)x''(s)+y'(s)y''(s)=0 .}

With these results, the acceleration can be found:

a(s)=ddtv(s){displaystyle mathbf {a} (s)={frac {mathrm {d} }{mathrm {d} t}}mathbf {v} (s)} =ddt[dsdt(x′(s), y′(s))] {displaystyle ={frac {mathrm {d} }{mathrm {d} t}}left[{frac {mathrm {d} s}{mathrm {d} t}}left(x'(s), y'(s)right)right] }

=(d2sdt2)ut(s)+(dsdt)2(x″(s), y″(s)){displaystyle =left({frac {mathrm {d} ^{2}s}{mathrm {d} t^{2}}}right)mathbf {u} _{mathrm {t} }(s)+left({frac {mathrm {d} s}{mathrm {d} t}}right)^{2}left(x''(s), y''(s)right)}

=(d2sdt2)ut(s)−(dsdt)21ρun(s) ,{displaystyle =left({frac {mathrm {d} ^{2}s}{mathrm {d} t^{2}}}right)mathbf {u} _{mathrm {t} }(s)-left({frac {mathrm {d} s}{mathrm {d} t}}right)^{2}{frac {1}{rho }}mathbf {u} _{mathrm {n} }(s) ,}

as can be verified by taking the dot product with the unit vectors u_t(s) and u_n(s). This result for acceleration is the same as that for circular motion based on the radius ρ. Using this coordinate system in the inertial frame, it is easy to identify the force normal to the trajectory as the centripetal force and that parallel to the trajectory as the tangential force. From a qualitative standpoint, the path can be approximated by an arc of a circle for a limited time, and for the limited time a particular radius of curvature applies, the centrifugal and Euler forces can be analyzed on the basis of circular motion with that radius.

This result for acceleration agrees with that found earlier. However, in this approach, the question of the change in radius of curvature with s is handled completely formally, consistent with a geometric interpretation, but not relying upon it, thereby avoiding any questions the image above might suggest about neglecting the variation in ρ.

Example: circular motion

To illustrate the above formulas, let x, y be given as:

x=αcos⁡sα ; y=αsin⁡sα .{displaystyle x=alpha cos {frac {s}{alpha }} ; y=alpha sin {frac {s}{alpha }} .}

Then:

x2+y2=α2 ,{displaystyle x^{2}+y^{2}=alpha ^{2} ,}

which can be recognized as a circular path around the origin with radius α. The position s = 0 corresponds to [α, 0], or 3 o'clock. To use the above formalism, the derivatives are needed:

y′(s)=cos⁡sα ; x′(s)=−sin⁡sα ,{displaystyle y^{prime }(s)=cos {frac {s}{alpha }} ; x^{prime }(s)=-sin {frac {s}{alpha }} ,}

y′′(s)=−1αsin⁡sα ; x′′(s)=−1αcos⁡sα .{displaystyle y^{prime prime }(s)=-{frac {1}{alpha }}sin {frac {s}{alpha }} ; x^{prime prime }(s)=-{frac {1}{alpha }}cos {frac {s}{alpha }} .}

With these results, one can verify that:

x′(s)2+y′(s)2=1 ; 1ρ=y′′(s)x′(s)−y′(s)x′′(s)=1α .{displaystyle x^{prime }(s)^{2}+y^{prime }(s)^{2}=1 ; {frac {1}{rho }}=y^{prime prime }(s)x^{prime }(s)-y^{prime }(s)x^{prime prime }(s)={frac {1}{alpha }} .}

The unit vectors can also be found:

ut(s)=[−sin⁡sα , cos⁡sα] ; un(s)=[cos⁡sα , sin⁡sα] ,{displaystyle mathbf {u} _{mathrm {t} }(s)=left[-sin {frac {s}{alpha }} , cos {frac {s}{alpha }}right] ; mathbf {u} _{mathrm {n} }(s)=left[cos {frac {s}{alpha }} , sin {frac {s}{alpha }}right] ,}

which serve to show that s = 0 is located at position [ρ, 0] and s = ρπ/2 at [0, ρ], which agrees with the original expressions for x and y. In other words, s is measured counterclockwise around the circle from 3 o'clock. Also, the derivatives of these vectors can be found:

ddsut(s)=−1α[cos⁡sα , sin⁡sα]=−1αun(s) ;{displaystyle {frac {mathrm {d} }{mathrm {d} s}}mathbf {u} _{mathrm {t} }(s)=-{frac {1}{alpha }}left[cos {frac {s}{alpha }} , sin {frac {s}{alpha }}right]=-{frac {1}{alpha }}mathbf {u} _{mathrm {n} }(s) ;}

 ddsun(s)=1α[−sin⁡sα , cos⁡sα]=1αut(s) .{displaystyle {frac {mathrm {d} }{mathrm {d} s}}mathbf {u} _{mathrm {n} }(s)={frac {1}{alpha }}left[-sin {frac {s}{alpha }} , cos {frac {s}{alpha }}right]={frac {1}{alpha }}mathbf {u} _{mathrm {t} }(s) .}

To obtain velocity and acceleration, a time-dependence for s is necessary. For counterclockwise motion at variable speed v(t):

s(t)=∫0t dt′ v(t′) ,{displaystyle s(t)=int _{0}^{t} dt^{prime } v(t^{prime }) ,}

where v(t) is the speed and t is time, and s(t = 0) = 0. Then:

v=v(t)ut(s) ,{displaystyle mathbf {v} =v(t)mathbf {u} _{mathrm {t} }(s) ,}

a=dvdtut(s)+vddtut(s)=dvdtut(s)−v1αun(s)dsdt{displaystyle mathbf {a} ={frac {mathrm {d} v}{mathrm {d} t}}mathbf {u} _{mathrm {t} }(s)+v{frac {mathrm {d} }{mathrm {d} t}}mathbf {u} _{mathrm {t} }(s)={frac {mathrm {d} v}{mathrm {d} t}}mathbf {u} _{mathrm {t} }(s)-v{frac {1}{alpha }}mathbf {u} _{mathrm {n} }(s){frac {mathrm {d} s}{mathrm {d} t}}}

a=dvdtut(s)−v2αun(s) ,{displaystyle mathbf {a} ={frac {mathrm {d} v}{mathrm {d} t}}mathbf {u} _{mathrm {t} }(s)-{frac {v^{2}}{alpha }}mathbf {u} _{mathrm {n} }(s) ,}

where it already is established that α = ρ. This acceleration is the standard result for non-uniform circular motion.

See also

Notes and references

Further reading

• 
  Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 978-0-534-40842-8.
  


• 
  Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 978-0-7167-0809-4.
  


• 
  Centripetal force vs. Centrifugal force, from an online Regents Exam physics tutorial by the Oswego City School District

External links

Look up centripetal in Wiktionary, the free dictionary.

• Notes from University of Winnipeg


• 
  Notes from Physics and Astronomy HyperPhysics at Georgia State University; see also home page
  


• Notes from Britannica


• Notes from PhysicsNet


• NASA notes by David P. Stern


• 
  Notes from U Texas.


• Analysis of smart yo-yo


• The Inuit yo-yo


• 
  Kinematic Models for Design Digital Library (KMODDL)
  Movies and photos of hundreds of working mechanical-systems models at Cornell University. Also includes an e-book library of classic texts on mechanical design and engineering.